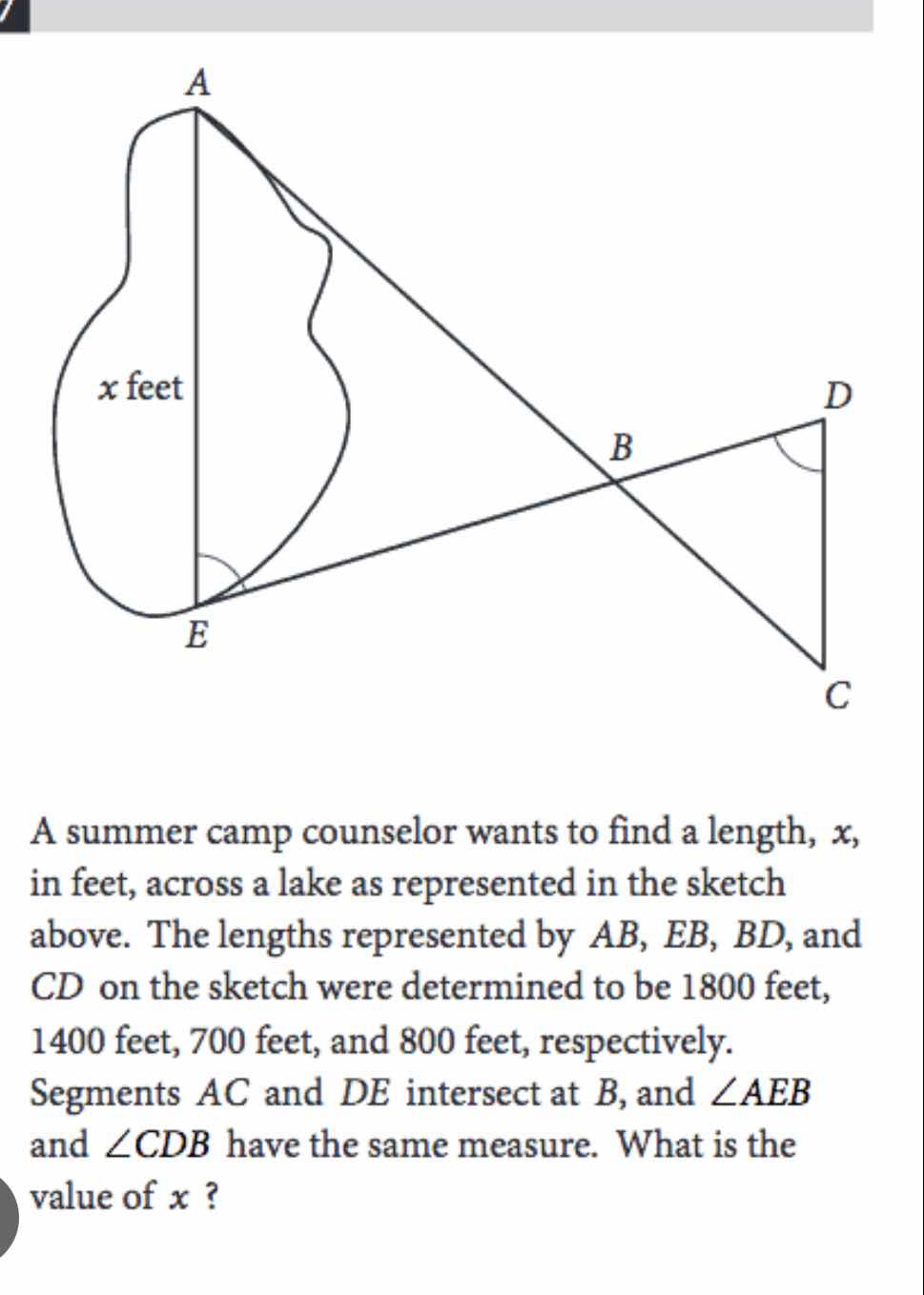
A summer camp counselor wants to find a length, x, in feet across a lake as represented in the sketch above. The lengths represented by AB, EB, BD, and CD on the sketch were determ... A summer camp counselor wants to find a length, x, in feet across a lake as represented in the sketch above. The lengths represented by AB, EB, BD, and CD on the sketch were determined to be 1800 feet, 1400 feet, 700 feet, and 800 feet, respectively. Segments AC and DE intersect at B, and ∠AEB and ∠CDB have the same measure. What is the value of x? Read more

Steps to Solve

1. Identify Known Lengths
   The lengths are given as follows:

• $AB = 1800$ feet
• $EB = 700$ feet
• $BD = 800$ feet
• $CD = 1400$ feet

2. Set Up Proportionality Using Similar Triangles
   Since $\angle AEB \cong \angle CDB$, triangles $AEB$ and $CDB$ are similar. This means the ratios of their corresponding sides are equal: $$ \frac{AB}{CD} = \frac{EB}{BD} = \frac{AE}{CB} $$

3. Substituting Known Values into the Ratio
   We can substitute the known lengths into the similarity ratio: $$ \frac{1800}{1400} = \frac{700}{800} $$

4. Simplify the Ratios
   Simplify both ratios: $$ \frac{1800 \div 200}{1400 \div 200} = \frac{700 \div 100}{800 \div 100} $$
   This simplifies to: $$ \frac{9}{7} = \frac{7}{8} $$

5. Setting Up the Expression for AE and CB
   Let $AE = x$ and $CB = 1800 - x$. Since $AB + EB = CD + BD$, we can express this as: $$ 1800 + 700 = 1400 + 800 $$

6. Solve for x
   Using the proportional sides, we set up: $$ \frac{x}{1800 - x} = \frac{7}{8} $$
   Cross-multiply to solve for $x$: $$ 8x = 7(1800 - x) $$
   Expanding this gives: $$ 8x = 12600 - 7x $$
   Combine like terms: $$ 15x = 12600 $$
   Thus, dividing by 15 gives: $$ x = \frac{12600}{15} = 840 $$