Solve using substitution. y = -9x - 9, y = -x + 7
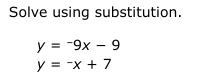
Understand the Problem
The question is asking to solve a system of equations using the substitution method. The user is provided with two equations in terms of y and x, and they are to find the values of x and y that satisfy both equations simultaneously.
Answer
The solution is $x = -2$ and $y = 9$.
Answer for screen readers
The solution to the system of equations is:
$$ x = -2, \quad y = 9 $$
Steps to Solve
- Substitute the first equation into the second We have the two equations:
$$ y = -9x - 9 $$
and
$$ y = -x + 7 $$
Substitute the expression for $y$ from the first equation into the second equation:
$$ -9x - 9 = -x + 7 $$
- Solve for x Now, we will solve for $x$.
First, rearrange the equation:
$$ -9x + x = 7 + 9 $$
This simplifies to:
$$ -8x = 16 $$
Now, divide both sides by -8:
$$ x = -2 $$
- Substitute x back to find y Next, we will substitute $x = -2$ back into one of the original equations to find $y$. We can use the first equation:
$$ y = -9(-2) - 9 $$
This simplifies to:
$$ y = 18 - 9 $$
which gives us:
$$ y = 9 $$
The solution to the system of equations is:
$$ x = -2, \quad y = 9 $$
More Information
The solution indicates the point of intersection between the two lines represented by the equations. In a graphical representation, this would be the point where the two lines cross.
Tips
- A common mistake is miscalculating when collecting like terms. Always double-check your arithmetic.
- Another mistake can occur when substituting values; ensure that you substitute into the correct equation.
AI-generated content may contain errors. Please verify critical information