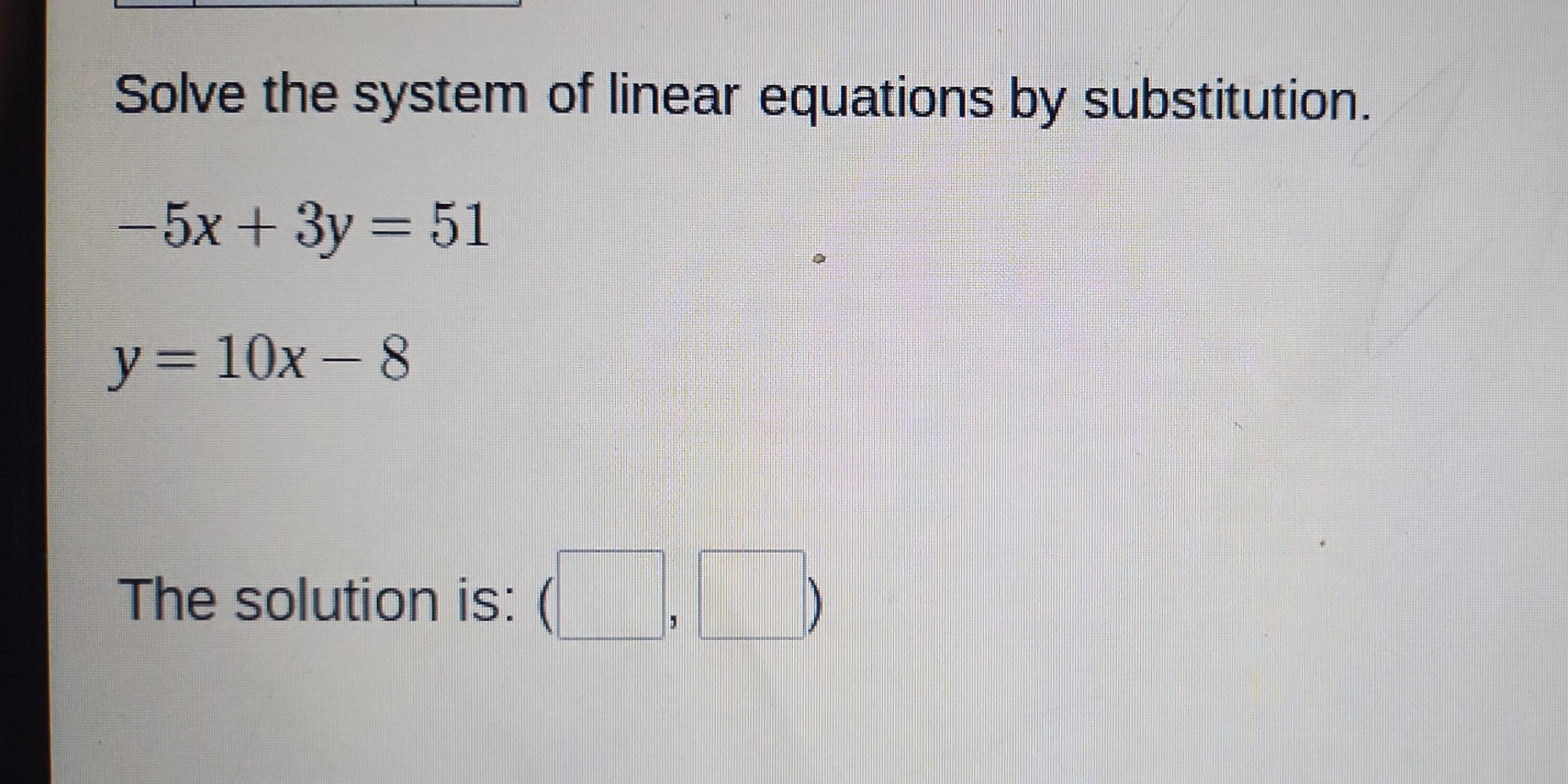
Solve the system of linear equations by substitution: -5x + 3y = 51, y = 10x - 8. The solution is: ( , )
Understand the Problem
The question is asking to solve a system of linear equations using the substitution method. The provided equations are -5x + 3y = 51 and y = 10x - 8. The goal is to find the values of x and y that satisfy both equations.
Answer
The solution is $(3, 22)$.
Answer for screen readers
The solution is $(3, 22)$.
Steps to Solve
- Substitute the value of y
Start with the second equation, which gives us a direct expression for $y$. Substitute $y = 10x - 8$ into the first equation:
$$ -5x + 3(10x - 8) = 51 $$
- Simplify the equation
Distribute the $3$ across the $(10x - 8)$:
$$ -5x + 30x - 24 = 51 $$
- Combine like terms
Now, combine $-5x$ and $30x$:
$$ 25x - 24 = 51 $$
- Solve for x
Add $24$ to both sides to isolate the term with $x$:
$$ 25x = 51 + 24 $$
Calculate the right side:
$$ 25x = 75 $$
Now, divide both sides by $25$:
$$ x = \frac{75}{25} = 3 $$
- Substitute x back to find y
Now that we have $x = 3$, substitute this value back into the equation for $y$:
$$ y = 10(3) - 8 $$
- Calculate y
Now calculate the value of $y$:
$$ y = 30 - 8 = 22 $$
The solution is $(3, 22)$.
More Information
The solution $(3, 22)$ indicates that when $x = 3$, the corresponding value of $y$ is $22$, satisfying both original equations.
Tips
- Forgetting to correctly distribute: When substituting and distributing, ensure each term is accounted for.
- Arithmetic errors: Double-check calculations, especially when combining like terms or performing addition and subtraction.
AI-generated content may contain errors. Please verify critical information