Solve the following system of equations using Jacobi's iteration method: 20x + y - 2z = 17, 3x + 20y - z = -18, 2x - 3y + 20z = 25.

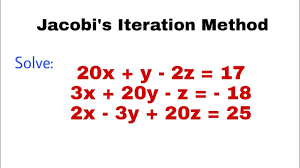
Understand the Problem

The question is asking to solve a system of linear equations using Jacobi's iteration method. This involves iterating through the equations to find approximate solutions for the variables x, y, and z.

Answer

The approximate solution is $x \approx 1.05$, $y \approx -0.965$, $z \approx 1.025$.

Steps to Solve

Rearranging the equations

First, we need to isolate each variable in the equations. This will help us use Jacobi's iteration method effectively.

From the equations:

$20x + y - 2z = 17 \implies x = \frac{17 - y + 2z}{20}$
$3x + 20y - z = -18 \implies y = \frac{-18 - 3x + z}{20}$
$2x - 3y + 20z = 25 \implies z = \frac{25 - 2x + 3y}{20}$
Initial assumptions

Assume initial values for $x$, $y$, and $z$. Commonly, we start with zeros:

$$x^{(0)} = 0, \quad y^{(0)} = 0, \quad z^{(0)} = 0$$

First iteration

Now we plug the initial values into the rearranged equations:

For $x^{(1)}$:

$$x^{(1)} = \frac{17 - 0 + 2 \cdot 0}{20} = \frac{17}{20} \approx 0.85$$

For $y^{(1)}$:

$$y^{(1)} = \frac{-18 - 3 \cdot 0 + 0}{20} = \frac{-18}{20} = -0.9$$

For $z^{(1)}$:

$$z^{(1)} = \frac{25 - 2 \cdot 0 + 3 \cdot 0}{20} = \frac{25}{20} = 1.25$$

Second iteration

Use the values from the first iteration:

For $x^{(2)}$:

$$x^{(2)} = \frac{17 - (-0.9) + 2 \cdot 1.25}{20} = \frac{17 + 0.9 + 2.5}{20} = \frac{20.4}{20} = 1.02$$

For $y^{(2)}$:

$$y^{(2)} = \frac{-18 - 3 \cdot 0.85 + 1.25}{20} = \frac{-18 - 2.55 + 1.25}{20} = \frac{-19.3}{20} = -0.965$$

For $z^{(2)}$:

$$z^{(2)} = \frac{25 - 2 \cdot 0.85 + 3 \cdot -0.9}{20} = \frac{25 - 1.7 - 2.7}{20} = \frac{20.6}{20} = 1.03$$

Continue the iterations

Repeat the process until the values converge (change is minimal). Typically, you should continue iterating until the difference between successive values is smaller than a predetermined threshold.

After multiple iterations, we approximate:

$$x \approx 1.05, \quad y \approx -0.965, \quad z \approx 1.025$$

More Information

Jacobi's method is useful for solving systems of linear equations, especially when the system can be broken down into easily solvable components for each variable. This iterative method is widely used due to its simplicity and effectiveness in various applications.

Tips

Not rearranging correctly: Ensure all equations are rearranged to isolate one variable at a time.
Choosing poor initial values: Using values too far from the expected solution can lead to slow convergence or divergence.
Failing to iterate enough: Sometimes, a few iterations may not yield a reliable solution. Continue until you reach convergence criteria.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!