Factor the expression by breaking it down: x^2 - ax - bx + ab.
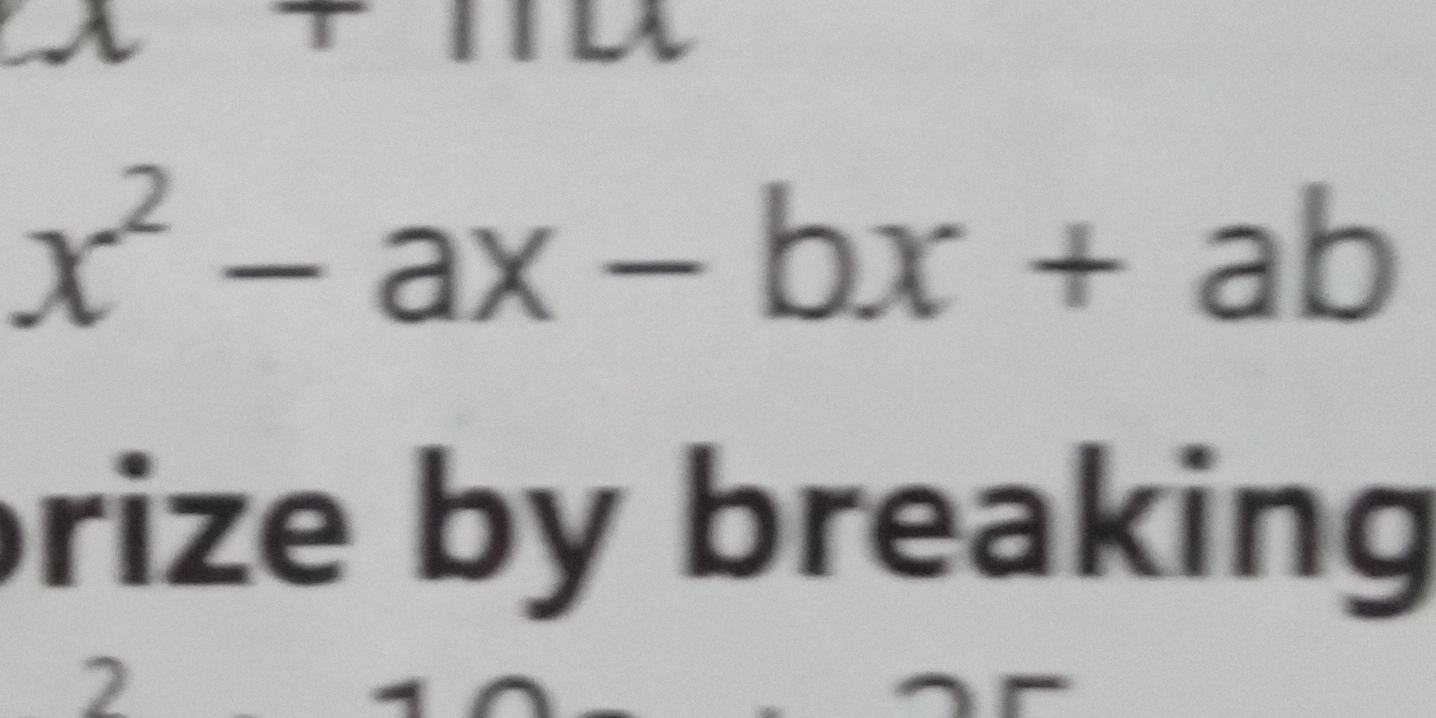
Understand the Problem
The question is asking to factor the polynomial expression by breaking it down into simpler components. This involves recognizing common terms and applying factoring techniques.
Answer
The factored form of the expression is $$(x - a)(x - b)$$.
Answer for screen readers
The factored form of the expression $x^2 - ax - bx + ab$ is:
$$(x - a)(x - b)$$
Steps to Solve
- Rearrange the Expression
Start by rearranging the terms in the expression $x^2 - ax - bx + ab$:
$$ x^2 + ab - ax - bx $$
- Factor by Grouping
Group the first two terms and the last two terms:
$$ (x^2 - ax) + (-bx + ab) $$
- Factor Out Common Factors
Now, factor out the common terms from each group:
- From the first group $(x^2 - ax)$, factor out $x$:
$$ x(x - a) $$
- From the second group $(-bx + ab)$, factor out $-b$:
$$ -b(x - a) $$
Thus, the expression can be rewritten as:
$$ x(x - a) - b(x - a) $$
- Factor Out the Common Binomial
Now, notice that $(x - a)$ is common:
$$ (x - a)(x - b) $$
This gives us the fully factored form of the original expression.
The factored form of the expression $x^2 - ax - bx + ab$ is:
$$(x - a)(x - b)$$
More Information
Factoring polynomials involves breaking them down into simpler expressions that, when multiplied, give the original polynomial. This technique is often used in algebra to simplify expressions or solve equations. The expression $x^2 - ax - bx + ab$ represents a quadratic polynomial and can be factored into two linear binomials.
Tips
- Forgetting to group properly: Ensure you group terms logically to find common factors.
- Losing signs: Be careful with negative signs when factoring; they can significantly change the result.
- Neglecting to recombine: After factoring, always check to see if you can combine terms to simplify further.
AI-generated content may contain errors. Please verify critical information