Sketch the region of integration for the integral ∫ from 0 to 2 ∫ from x^2 to 2x (4x + 2) dy dx and write an equivalent integral with the order of integration reversed.
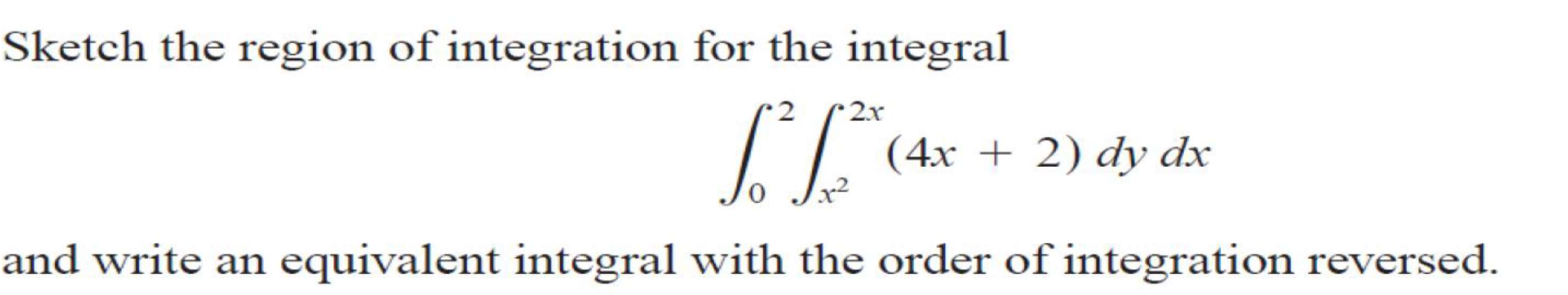
Understand the Problem
The question is asking to sketch the region of integration defined by the given double integral and to find an equivalent integral with the order of integration reversed. This involves understanding the bounds given for both x and y in the integral and how to represent them graphically.
Answer
$$ \int_{0}^{4} \int_{\sqrt{y}}^{\frac{y}{2}} (4x + 2) \, dx \, dy $$
Answer for screen readers
$$ \int_{0}^{4} \int_{\sqrt{y}}^{\frac{y}{2}} (4x + 2) , dx , dy $$
Steps to Solve
-
Identify the bounds for integration
The double integral is defined as:
$$ \int_{0}^{2} \int_{x^2}^{2x} (4x + 2) , dy , dx $$
The outer integration is with respect to (x), ranging from 0 to 2, and the inner integration is with respect to (y), ranging from (x^2) to (2x). -
Sketching the region of integration
To sketch the region, first plot the boundaries given by the equations (y = x^2) and (y = 2x):
- For (y = x^2), this is a parabola opening upwards.
- For (y = 2x), this is a straight line through the origin with a slope of 2.
Find their points of intersection by setting:
$$ x^2 = 2x $$
$$ x^2 - 2x = 0 $$
Factoring gives:
$$ x(x - 2) = 0 $$
Thus, the points of intersection are (x = 0) and (x = 2). Plot these points on the graph.
-
Plot the graph
Begin by marking the bounds on the (x)-axis (from 0 to 2) and the respective curves. The region of integration is below the line (y = 2x) and above the curve (y = x^2) between (x = 0) and (x = 2). -
Express the integral with reversed order of integration
To reverse the order of integration, identify the new limits:
- (y) ranges from the lowest (y) value (which occurs at (x = 0) and (x = 2)):
- At (x = 0): (y = 0) (from (y = x^2)).
- At (x = 2): (y = 4) (from (y = 2x)).
Thus, (y) ranges from 0 to 4.
Now, find (x) bounds for each (y):
- When (y) is between 0 and 4:
- From (y = x^2): (x = \sqrt{y})
- From (y = 2x): (x = \frac{y}{2})
The new integral, with (y) as the outer variable and (x) as the inner variable, is:
$$ \int_{0}^{4} \int_{\sqrt{y}}^{\frac{y}{2}} (4x + 2) , dx , dy $$
$$ \int_{0}^{4} \int_{\sqrt{y}}^{\frac{y}{2}} (4x + 2) , dx , dy $$
More Information
This reverse integral swaps the order of integration from first integrating (y) over its bounds for each value of (x) to integrating (x) over its bounds for each value of (y). It efficiently captures the same area under the curve defined by the original double integral.
Tips
- Incorrectly identifying the limits: Make sure to check the intersections carefully, and always verify the bounds for both variables after sketching.
- Confusing the curves: Remember the orientation of the curves and which one is upper and lower when plotting to avoid errors in the integration limits.
AI-generated content may contain errors. Please verify critical information