Sketch a possible graph of a function that satisfies the conditions below. f(0) = -1; lim f(x) = 0 as x approaches 0-; lim f(x) = -1 as x approaches 0+.
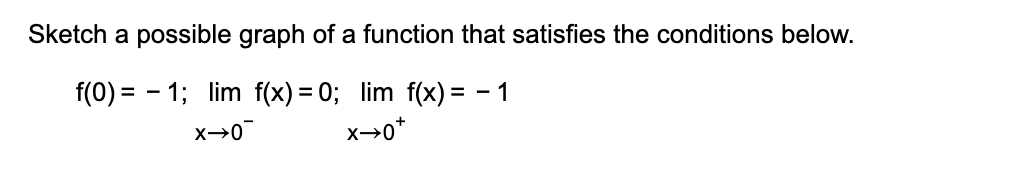
Understand the Problem
The question is asking to sketch a graph of a function based on specific limit and function value conditions: the function must equal -1 at zero, approach zero as x approaches zero from the left, and approach -1 as x approaches zero from the right.
Answer
A possible graph features a point at \( (0, -1) \), a curve approaching \( 0 \) from the left, and a line approaching \( -1 \) from the right.
Answer for screen readers
The graph sketched would feature a point at ((0, -1)), a rising curve approaching ( 0 ) from the left, and a line approaching ( -1 ) from the right.
Steps to Solve
-
Identify the Conditions Given The function must satisfy three key conditions:
- ( f(0) = -1 ) (the function value at zero).
- ( \lim_{x \to 0^-} f(x) = 0 ) (the limit as ( x ) approaches zero from the left).
- ( \lim_{x \to 0^+} f(x) = -1 ) (the limit as ( x ) approaches zero from the right).
-
Sketch the Graph Around ( x = 0 )
- At ( x = 0 ), the graph must go to ( -1 ) since ( f(0) = -1 ).
- As ( x ) approaches ( 0 ) from the left (negative direction), the graph should approach ( 0 ).
- As ( x ) approaches ( 0 ) from the right (positive direction), the graph should approach ( -1 ).
-
Draw the Left Side of the Graph
- For ( x < 0 ), draw the graph approaching ( 0 ) as it reaches ( 0 ) from the left. This can be a simple curve or line that gradually rises toward the point ((0, 0)).
-
Draw the Right Side of the Graph
- For ( x > 0 ), draw the graph that approaches ( -1 ) as it reaches ( 0 ) from the right. This can also be a line or curve that starts just below ( -1 ) and approaches it as ( x ) gets closer to ( 0 ).
-
Indicate Discontinuity
- Make sure there is clearly a point at ((0, -1)) on the graph, as this represents the function value at ( 0 ).
The graph sketched would feature a point at ((0, -1)), a rising curve approaching ( 0 ) from the left, and a line approaching ( -1 ) from the right.
More Information
This sketch illustrates a simple piecewise function that meets the conditions specified. One possible function that satisfies these conditions could be defined piecewise around zero.
Tips
- Confusing the limits: Ensure that left and right limits are accurately described. It's important to identify and label the approach from both sides separate from the actual function value at ( 0 ).
- Not indicating the point value properly: Be clear on where the function is defined, especially at the point where it jumps or is discontinuous.
AI-generated content may contain errors. Please verify critical information