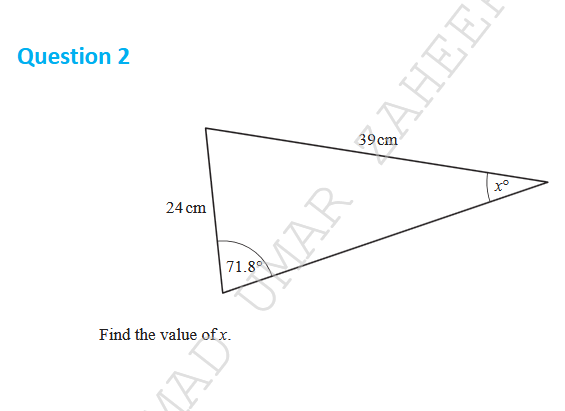
Find the value of x.

Steps to Solve

1. Identify the known angles and side lengths

In the triangle, we know one angle measures $71.8^\circ$ and the other angle is $x$. The side opposite the angle $x$ is $39 , cm$ and the side opposite the $71.8^\circ$ angle is $24 , cm$.

2. Use the triangle angle sum property

The sum of the angles in a triangle is always $180^\circ$. Therefore, we can find the value of $x$ by using the equation:

$$ x + 71.8^\circ + \text{other angle} = 180^\circ $$

3. Calculate the other angle using the Law of Sines

We can set up the Law of Sines:

$$ \frac{a}{\sin A} = \frac{b}{\sin B} $$

Where:

• $a = 39 , cm$ (opposite angle $x$)
• $b = 24 , cm$ (opposite angle $71.8^\circ$)
• $A = x$
• $B = 71.8^\circ$

Thus, we can rewrite it as:

$$ \frac{39}{\sin x} = \frac{24}{\sin 71.8^\circ} $$

4. Solve for $\sin x$

Rearranging the equation gives us:

$$ \sin x = \frac{39 \cdot \sin 71.8^\circ}{24} $$

5. Calculate angle $x$

Now compute $x$ by taking the inverse sine:

$$ x = \arcsin\left(\frac{39 \cdot \sin 71.8^\circ}{24}\right) $$

6. Substituting the values

First calculate $\sin 71.8^\circ$, then substitute it in:

$$ x = \arcsin\left(\frac{39 \cdot 0.9553}{24}\right) $$

7. Final computation to find $x$

Calculating that gives us the value of $x$.