Show that the equation x^3 + 3x + 1 = 0 has exactly one real solution.

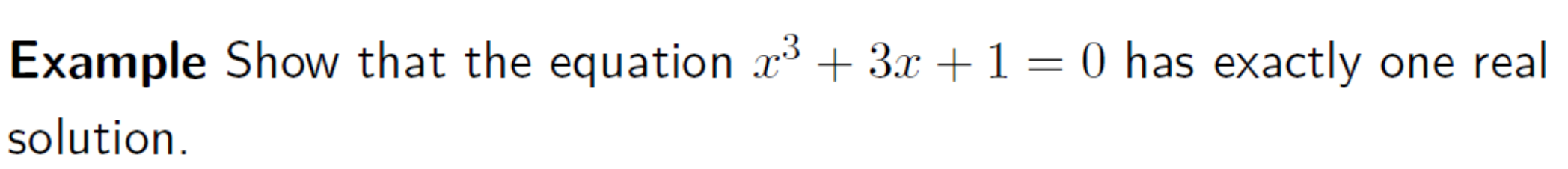
Understand the Problem

The question is asking to demonstrate that the cubic equation x^3 + 3x + 1 = 0 has only one real solution. This may involve analysis of the function's behavior, such as its derivatives or graph.

Answer

The equation $ x^3 + 3x + 1 = 0 $ has exactly one real solution.

Steps to Solve

Define the function

Let ( f(x) = x^3 + 3x + 1 ). We will analyze this function to determine its behavior and find its roots.

Find the derivative

Calculate the derivative of ( f(x) ). This helps us understand the function's behavior:

$$ f'(x) = 3x^2 + 3 $$

Analyze the derivative

Notice that ( f'(x) = 3(x^2 + 1) ). Since ( x^2 + 1 > 0 ) for all real ( x ), it follows that:

$$ f'(x) > 0 $$

This means ( f(x) ) is strictly increasing everywhere.

Check for real roots

Since ( f(x) ) is strictly increasing, it can cross the x-axis at most once. We can evaluate:

( f(-1) = (-1)^3 + 3(-1) + 1 = -1 - 3 + 1 = -3 ) (negative value)
( f(0) = 0^3 + 3(0) + 1 = 1 ) (positive value)

Here, ( f(-1) < 0 ) and ( f(0) > 0 ) indicate that there is at least one real solution between (-1) and (0).

Conclude uniqueness of the solution

Since ( f(x) ) is strictly increasing, the function can only cross the x-axis once. Therefore, the cubic equation ( x^3 + 3x + 1 = 0 ) has exactly one real solution.

The equation ( x^3 + 3x + 1 = 0 ) has exactly one real solution.

More Information

This conclusion is based on the properties of polynomial functions, particularly cubics, which can have at most three real roots. The strictly increasing nature of this function ensures that it will touch the x-axis only once.

Tips

Assuming that the function can have multiple real solutions without checking the derivative.
Miscalculating function values when checking for sign changes. Always ensure you compute correctly.

Thank you for voting!