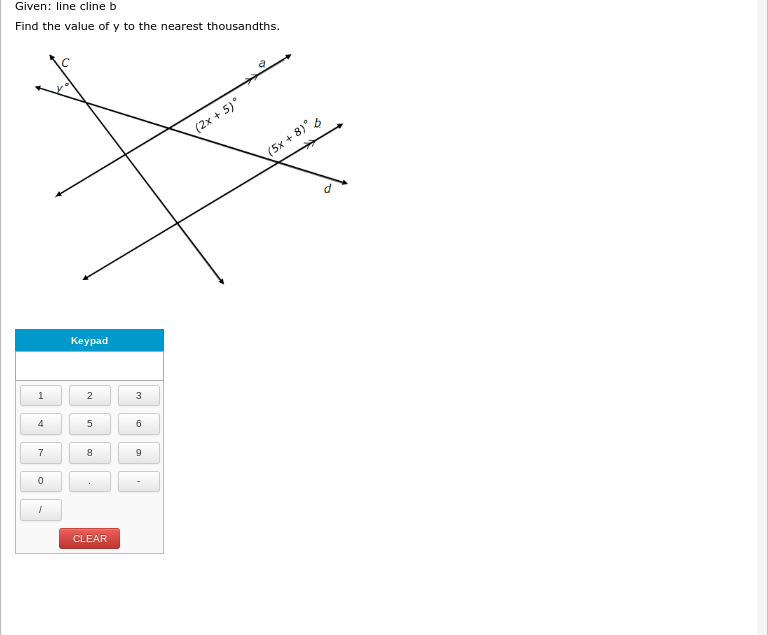
Given: line c line b. Find the value of y to the nearest thousandths.
Understand the Problem
The question is asking to find the value of the variable y based on the angles formed by intersecting lines, where certain angles are expressed in terms of x. We need to set up an equation using the properties of angles created by transversal lines and solve for y.
Answer
The value of \( y \) is \( 3 \).
Answer for screen readers
The value of ( y ) is ( 3 ).
Steps to Solve
- Identify the angles formed by the intersecting lines
The angles formed are given by ( (2x + 5)^\circ ) and ( (5x + 8)^\circ ), as well as ( y^\circ ).
- Use the properties of angles
Since angles ( (2x + 5)^\circ ) and ( (5x + 8)^\circ ) are vertically opposite, they will be equal: $$ 2x + 5 = 5x + 8 $$
- Rearrange the equation to solve for x
Subtract ( 2x ) and ( 8 ) from both sides to isolate ( x ): $$ 5 - 8 = 5x - 2x $$ This simplifies to: $$ -3 = 3x $$
- Solve for x
Divide both sides by 3: $$ x = -1 $$
- Substitute x back into the expression for y
Now substitute ( x = -1 ) into the expression for ( y ): $$ y = 5x + 8 $$ $$ y = 5(-1) + 8 $$ This simplifies to: $$ y = -5 + 8 = 3 $$
The value of ( y ) is ( 3 ).
More Information
This problem illustrates how to solve for unknown variables using properties of angles, specifically the equality of vertically opposite angles. The final answer, ( y = 3 ), is calculated through a simple algebraic process.
Tips
- Failing to recognize that vertically opposite angles are equal can lead to incorrect equations.
- Not correctly rearranging equations can result in errors in solving for ( x ).
- Substituting the wrong value of ( x ) back into the equation for ( y ), yielding incorrect results.
AI-generated content may contain errors. Please verify critical information