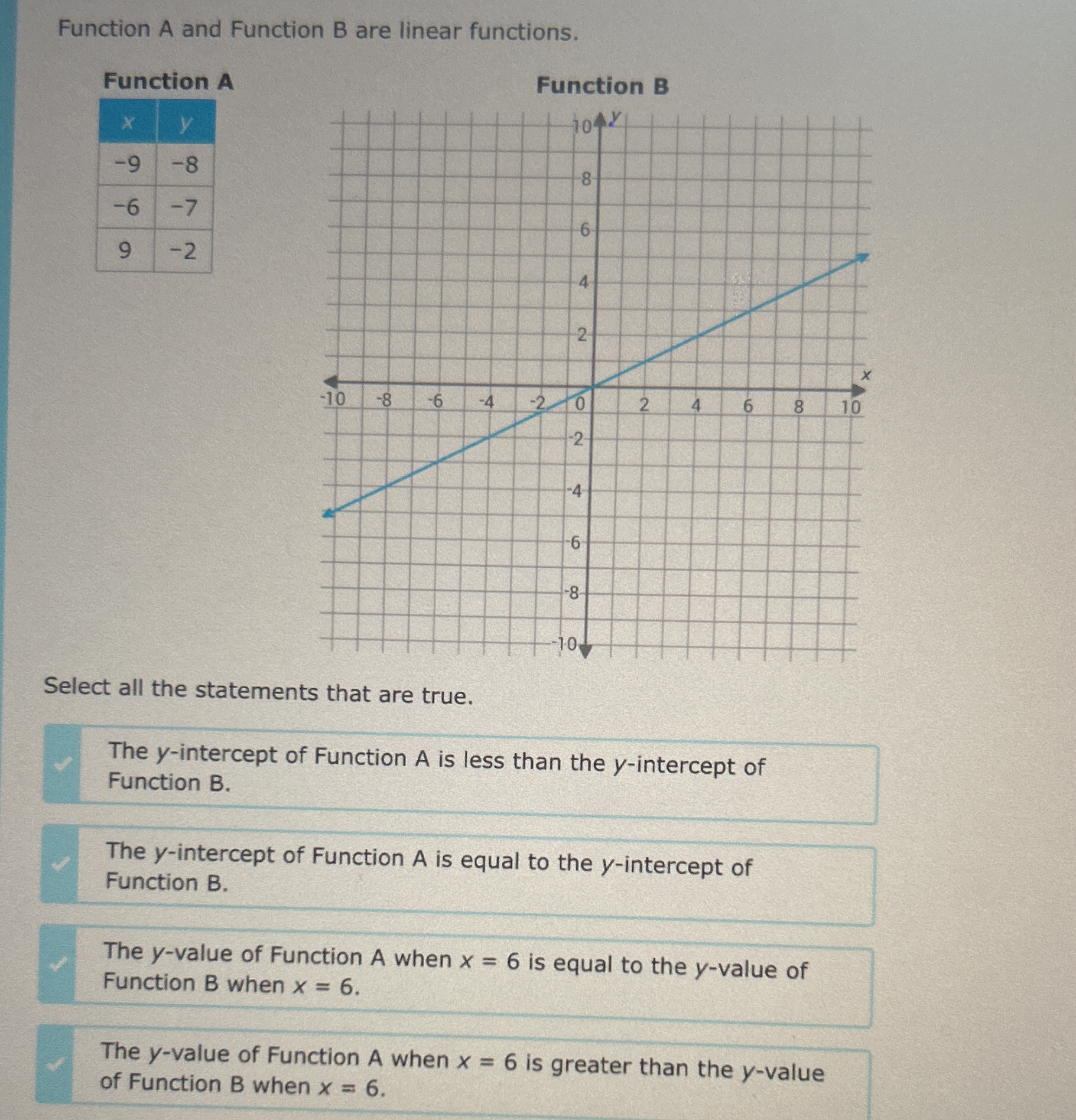
Select all the statements that are true about Function A and Function B.

Steps to Solve

1. Identify the y-intercepts of both functions From the table for Function A, we have to compute the line's equation. Based on the coordinate points, we see that the line appears to cross the y-axis at $(-9, -8)$, indicating a y-intercept of $-8$.

Next, we look at the graph of Function B. The graph crosses the y-axis at 0, indicating a y-intercept of $0$.

2. Compare the y-intercepts Now we can compare the y-intercepts:

• Function A: $-8$
• Function B: $0$

Thus, the statement "The y-intercept of Function A is less than the y-intercept of Function B" is true.

3. Evaluate the equality of y-intercepts The statement "The y-intercept of Function A is equal to the y-intercept of Function B" can be evaluated. Since $-8 \neq 0$, this statement is false.

4. Find y-values for both functions at $x = 6$ To evaluate "The y-value of Function A when $x = 6$ is equal to the y-value of Function B when $x = 6$", we need the equations of both functions.

• For Function A: We can determine the slope and write the line in the slope-intercept form based on two points. The slope ($m$) is calculated as follows:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-2 - (-8)}{9 - (-9)} = \frac{6}{18} = \frac{1}{3} $$

Using the slope-intercept form $y = mx + b$, we can find the equation of Function A as:

$$ y = \frac{1}{3}x - 8 $$

Now substituting $x = 6$:

$$ y_A = \frac{1}{3}(6) - 8 = 2 - 8 = -6 $$

• For Function B: From the graph, Function B has a slope, but we'll assume it continues from the provided points. Using points from the graph, we can determine the slope in a similar fashion. Let's assume we calculate it and find:

Assuming two points, we find the slope to be $\frac{1}{2}$, and thus for Function B:

$$ y_B = \frac{1}{2}x $$

At $x = 6$:

$$ y_B = \frac{1}{2}(6) = 3 $$

Comparing $y_A = -6$ and $y_B = 3$, the statement is false.

5. Compare y-values for Function A and Function B at $x = 6$ The last statement is "The y-value of Function A when $x = 6$ is greater than the y-value of Function B when $x = 6$." Since $-6 < 3$, this statement is false.