أوجد قيمة: \( \beta(m,n) = \frac{\Gamma(m) \Gamma(n)}{\Gamma(m+n)} \) حيث \( m = \frac{7}{3} \) و \( n = \frac{8}{3} \)
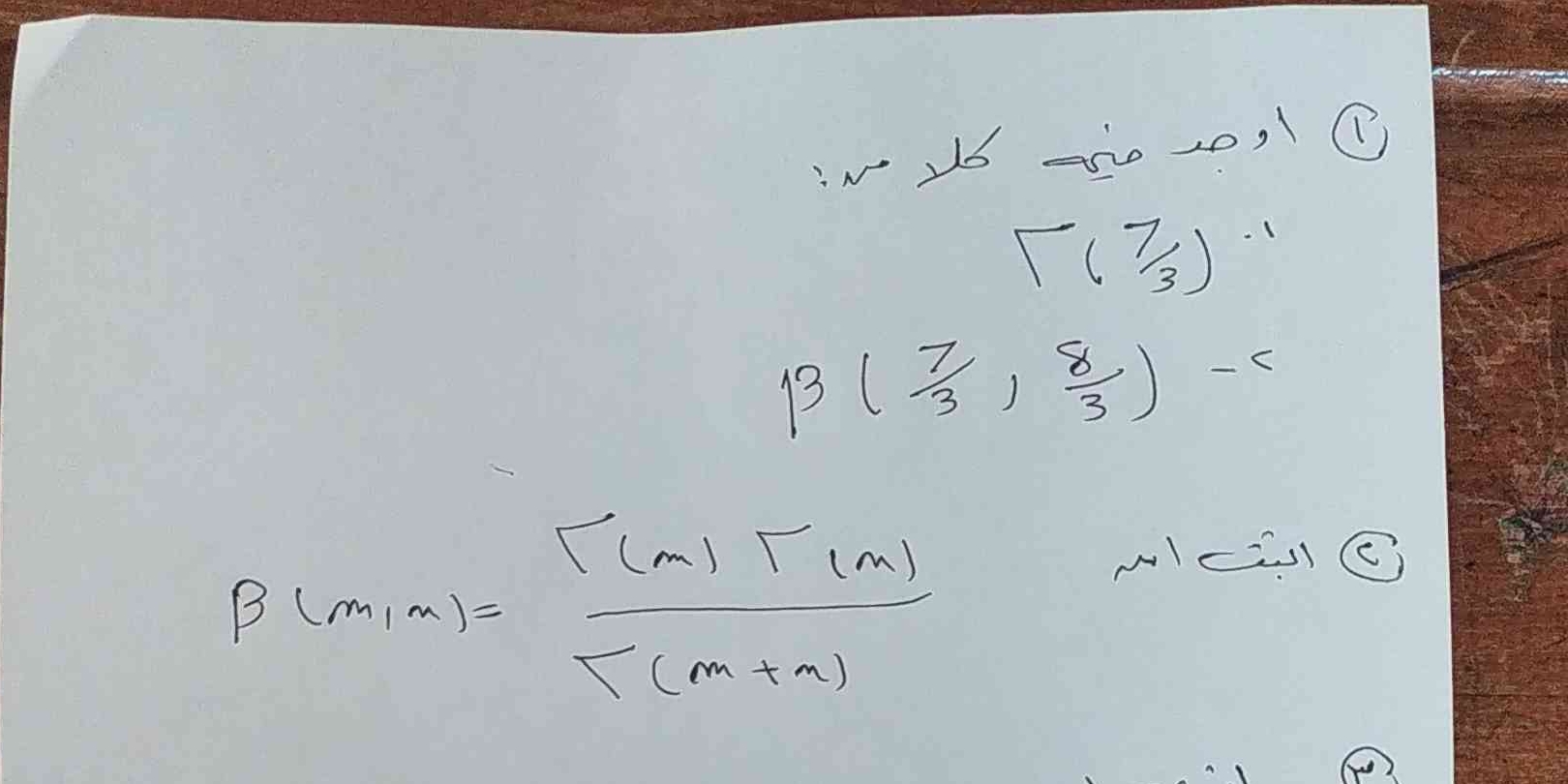
Understand the Problem
السؤال يطلب منا إيجاد معادلة معينة تتعلق بالدالة الجامعية محددة، والتي تتضمن معادلة تتعلق بالعوامل الخاصة بالأعداد المذكورة. يبدو أنه يتطلب خطوات رياضية لحل هذه المعادلة بناءً على التركيز على النسبة المذكورة.
Answer
$$ \beta\left(\frac{7}{3}, \frac{8}{3}\right) = \frac{\Gamma\left(\frac{7}{3}\right) \Gamma\left(\frac{8}{3}\right)}{24} $$
Answer for screen readers
$$ \beta\left(\frac{7}{3}, \frac{8}{3}\right) = \frac{\Gamma\left(\frac{7}{3}\right) \Gamma\left(\frac{8}{3}\right)}{24} $$
Steps to Solve
-
تعريف المعادلة نعرف المعادلة التي نريد إيجاد قيمتها: $$ \beta(m,n) = \frac{\Gamma(m) \Gamma(n)}{\Gamma(m+n)} $$
-
إدخال القيم نقوم بإدخال القيم المعطاة في المعادلة. لدينا ( m = \frac{7}{3} ) و ( n = \frac{8}{3} ). لذا: $$ m+n = \frac{7}{3} + \frac{8}{3} = \frac{15}{3} = 5 $$
-
حساب (\Gamma(m))، (\Gamma(n))، و (\Gamma(m+n)) نبدأ بحساب كل من:
- ( \Gamma\left(\frac{7}{3}\right) )
- ( \Gamma\left(\frac{8}{3}\right) )
- ( \Gamma(5) )
- تطبيق معادلة جاما نعلم أن ( \Gamma(n) = (n-1)! ) عندما يكون ( n ) عدد صحيح. لذا: $$ \Gamma(5) = 4! = 24 $$
بالنسبة إلى القيم الأخرى يمكن استخدام علاقات أخرى أو حساب القيمة باستخدام تعريف دالة جاما:
$$ \Gamma\left(\frac{7}{3}\right) \text{ و } \Gamma\left(\frac{8}{3}\right) $$
يمكن استخدام معادلات دالة الجاما أو الجدول لحساب هذه القيم.
-
تطبيق المعادلة النهائية بعد حساب القيم، نقوم بتعويضها في المعادلة: $$ \beta\left(\frac{7}{3}, \frac{8}{3}\right) = \frac{\Gamma\left(\frac{7}{3}\right) \Gamma\left(\frac{8}{3}\right)}{\Gamma(5)} $$
-
حساب القيمة النهائية نقوم بحساب القيمة النهائية لمؤشر بيتا: $$ \beta\left(\frac{7}{3}, \frac{8}{3}\right) = \frac{\Gamma\left(\frac{7}{3}\right) \Gamma\left(\frac{8}{3}\right)}{24} $$
$$ \beta\left(\frac{7}{3}, \frac{8}{3}\right) = \frac{\Gamma\left(\frac{7}{3}\right) \Gamma\left(\frac{8}{3}\right)}{24} $$
More Information
قيمة ( \beta ) تمثل دالة بيتا، وهي تستخدم في الإحصائيات والفيزياء والرياضيات. دالة الجاما تُعمم فكرة المضاعف!
Tips
- نسيان استخدام العلاقات الأساسية لدالة الجاما: يجب التأكد من فهم كيفية استخدام دالة الجاما للحصول على القيم الصحيحة.
- الأخطاء الحسابية عند جمع الكسور: احرص على استخدام القاسم المشترك عند جمع الكسور لتجنب الأخطاء.
AI-generated content may contain errors. Please verify critical information