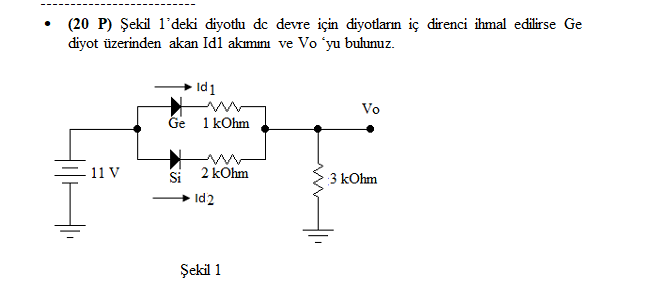
Şekil 1'deki diyotlu dc devrede, diyotların iç direnci ihmal edilirse Ge diyot üzerinden akan Id1 akımını ve Vo'yu bulunuz.

Steps to Solve

1. Devreyi Analiz Etme

Verilen devrede, diyotların iç direnci ihmal edildiği için diyotlar tam iletimde kabul edilir. Bu durumda diyotların gerilim düşüşü sıfırdır.

2. Kullanılan Dirençleri Belirleme

Devredeki dirençler:

• $R_1 = 1 , k\Omega$ (Ge diyotu üzerinden)
• $R_2 = 2 , k\Omega$ (Si diyotu üzerinden)
• $R_3 = 3 , k\Omega$ (Yük direnci)

3. Devre Akımını Hesaplama

Toplam direncimizi ve akımımızı bulmak için toplam devreyi inceleyelim. Ge diyotu ve Si diyotu paralel bağlıdır.

Toplam direnç $R_{paralel}$:

$$ \frac{1}{R_{paralel}} = \frac{1}{R_1} + \frac{1}{R_2} = \frac{1}{1000} + \frac{1}{2000} $$

Hesaplama:

$$ \frac{1}{R_{paralel}} = \frac{2 + 1}{2000} = \frac{3}{2000} $$

Bu durumda $R_{paralel} = \frac{2000}{3} , \Omega$ olur.

4. Toplam Direnci Bulma

Toplam direnç devredeki yük direnci ile paralel dirençlerin toplamı:

$$ R_{toplam} = R_{paralel} + R_3 = \frac{2000}{3} + 3000 $$

Hesaplama:

$$ R_{toplam} = \frac{2000}{3} + \frac{9000}{3} = \frac{11000}{3} , \Omega $$

5. Devreden Geçen Akımı Hesaplama

Total devre akımını bulmak için toplam gerilim kaynakları ve toplam direnci kullanarak:

$$ I_{total} = \frac{V}{R_{toplam}} = \frac{11}{\frac{11000}{3}} = \frac{11 \times 3}{11000} $$

Hesaplama:

$$ I_{total} = \frac{33}{11000} = 0.003 , A = 3 , mA $$

6. Ge Diyotu Üzerinden Akan Akımı Hesaplama

Diyotlar paralel bağlı olduğu için akımları paylaşır. Ge diyotu üzerinden akan akım $I_{d1}$ ve Si diyotu üzerinden akan akım $I_{d2}$ şöyle yazılabilir:

$$ I_{d1} = I_{total} \cdot \frac{R_2}{R_1 + R_2} $$

$$ I_{d1} = 0.003 \cdot \frac{2000}{1000 + 2000} = 0.003 \cdot \frac{2}{3} $$

Hesaplama sonucu:

$$ I_{d1} = 0.002 , A = 2 , mA $$

7. Vo Gerilimini Hesaplama

Son olarak, yük direnci üzerindeki gerilim (V_o) şu şekilde hesaplanır:

$$ V_o = I_{d1} \cdot R_3 = 0.002 \cdot 3000 = 6 , V $$