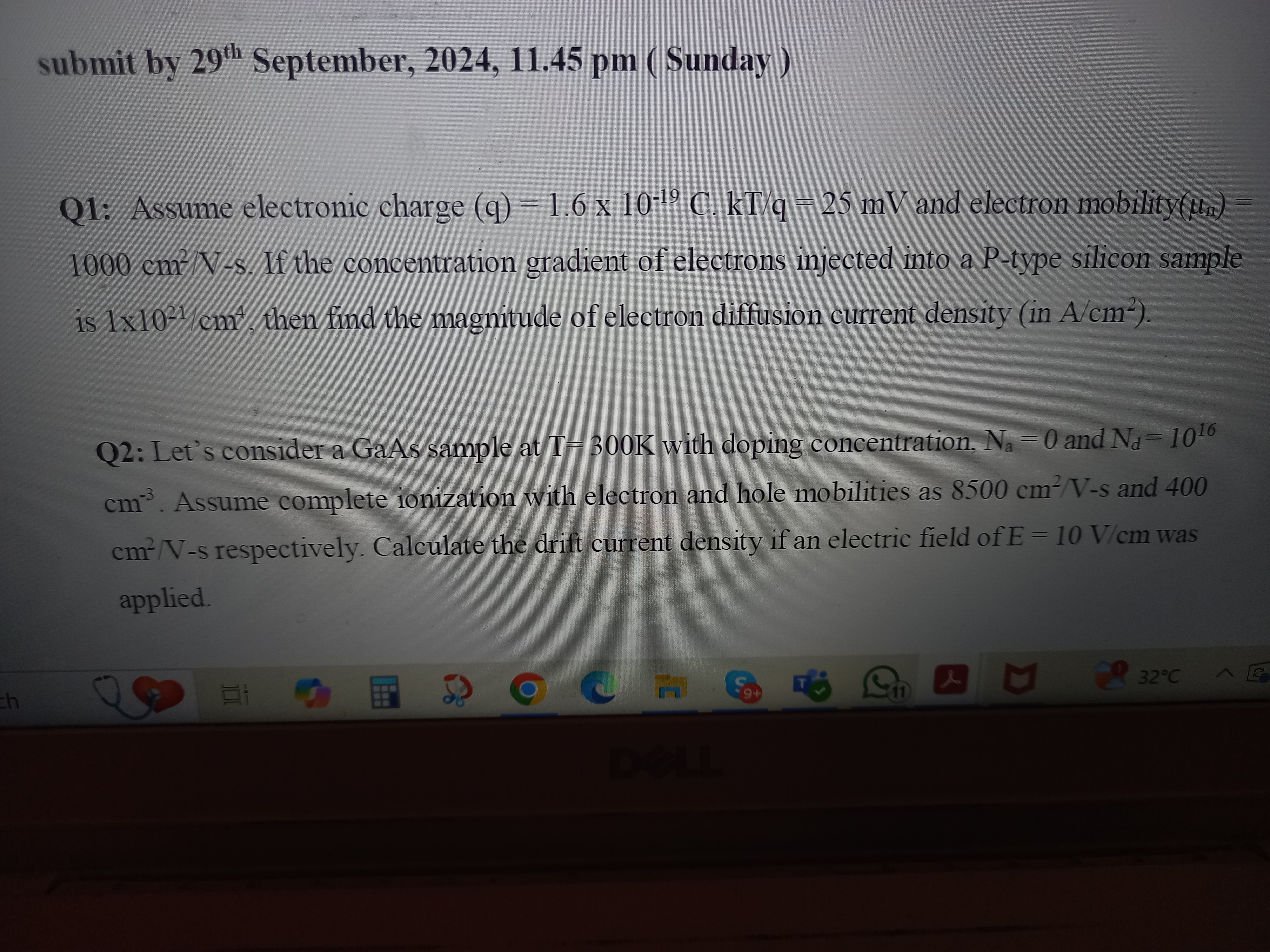
Q1: Assume electronic charge (q) = 1.6 x 10^-19 C, kT/q = 25 mV and electron mobility (μn) = 1000 cm^2/V-s. If the concentration gradient of electrons injected into a P-type silico... Q1: Assume electronic charge (q) = 1.6 x 10^-19 C, kT/q = 25 mV and electron mobility (μn) = 1000 cm^2/V-s. If the concentration gradient of electrons injected into a P-type silicon sample is 1x10^21/cm^4, then find the magnitude of electron diffusion current density (in A/cm^2). Q2: Let’s consider a GaAs sample at T= 300K with doping concentration, Na = 0 and Nd = 10^16 cm^-3. Assume complete ionization with electron and hole mobilities as 8500 cm^2/V-s and 400 cm^2/V-s respectively. Calculate the drift current density if an electric field of E = 10 V/cm was applied. Read more

Steps to Solve

1. Calculate the Electron Diffusion Current Density for Q1

The formula for the electron diffusion current density ($J_n$) is given by:

$$ J_n = -q D_n \frac{d(n)}{dx} $$

Where:

• $q = 1.6 \times 10^{-19}$ C (electron charge)
• $D_n$ is the diffusion constant, which can be found using the mobility ($\mu_n$) and the thermal voltage ($V_T$):

$$ D_n = \mu_n \cdot kT/q $$

For silicon:

• $\mu_n = 1000 , \text{cm}^2/\text{V-s}$
• Assuming room temperature, $kT/q \approx 25 , \text{mV} = 0.025 , \text{V}$

Now calculate $D_n$:

$$ D_n = 1000 , \text{cm}^2/\text{V-s} \cdot 0.025 , \text{V} = 25 , \text{cm}^2/\text{s} $$

Next, the concentration gradient $\frac{d(n)}{dx}$ is given as $1 \times 10^{21} , \text{cm}^{-4}$.

Now substitute these values into the equation for $J_n$:

$$ J_n = -1.6 \times 10^{-19} \cdot 25 \cdot (1 \times 10^{21}) = -4 , \text{A/cm}^2 $$

2. Calculate the Drift Current Density for Q2

The drift current density ($J_d$) is given by:

$$ J_d = q n \mu_n E $$

For GaAs:

• The electron concentration, $n$, is equal to the donor concentration $N_d = 10^{16} , \text{cm}^{-3}$, as $N_a = 0$.
• $\mu_n = 8500 , \text{cm}^2/\text{V-s}$
• The electric field, $E = 10 , \text{V/cm}$

Now substitute these values:

$$ J_d = (1.6 \times 10^{-19}) \cdot (10^{16}) \cdot (8500) \cdot (10) = 1.36 , \text{A/cm}^2 $$