y is directly proportional to the square of (x - 1). y = 63 when x = 4. Find the value of y when x = 6.

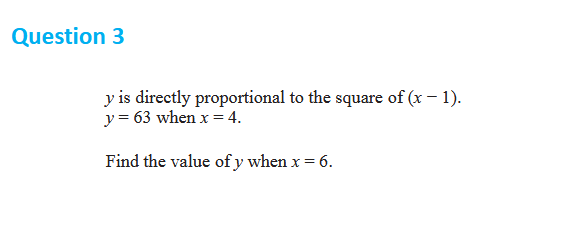
Understand the Problem

The question is asking us to find the value of y when x = 6, given that y is directly proportional to the square of (x - 1) and that y equals 63 when x is 4. To solve this, we will establish the relationship between y and x using the direct proportionality condition and then calculate y for x = 6.

Answer

The value of $ y $ when $ x = 6 $ is $ y = 175 $.

Steps to Solve

Establish the proportional relationship

Since ( y ) is directly proportional to the square of ( (x - 1) ), we can express this relationship as:

$$ y = k(x - 1)^2 $$

where ( k ) is the proportionality constant.

Determine the value of ( k )

We know from the problem that ( y = 63 ) when ( x = 4 ). Substituting these values into the equation:

$$ 63 = k(4 - 1)^2 $$

This simplifies to:

$$ 63 = k(3^2) $$

which gives:

$$ 63 = 9k $$

Solving for ( k ):

$$ k = \frac{63}{9} = 7 $$

Substitute ( k ) back into the equation

Now that we have ( k ), we can rewrite the equation for ( y ):

$$ y = 7(x - 1)^2 $$

Calculate ( y ) when ( x = 6 )

Substituting ( x = 6 ) into the equation:

$$ y = 7(6 - 1)^2 $$

This simplifies to:

$$ y = 7(5^2) $$

Calculating further:

$$ y = 7 \times 25 $$

Final calculation

Completing the multiplication gives:

$$ y = 175 $$

The value of ( y ) when ( x = 6 ) is ( y = 175 ).

More Information

In problems involving direct proportionality, it’s crucial to first find the proportionality constant by using initial conditions. Here, we found ( k = 7 ), which allowed us to compute ( y ) for any value of ( x ) based on our established relationship.

Tips

Forgetting to square ( (x - 1) ): Ensure to follow the problem’s specifications about squaring the expression correctly.
Miscalculating the proportionality constant: Double-check calculations to avoid arithmetic errors.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!