Prove each identity. a) cos x tan^3 x = sin x tan^2 x b) sin^2 θ + cos^4 θ = cos^2 θ + sin^4 θ c) (sin x + cos x)(tan^2 x + 1) / tan x = 1 / cos x + 1 / sin x d) tan^2 β + cos^2 β... Prove each identity. a) cos x tan^3 x = sin x tan^2 x b) sin^2 θ + cos^4 θ = cos^2 θ + sin^4 θ c) (sin x + cos x)(tan^2 x + 1) / tan x = 1 / cos x + 1 / sin x d) tan^2 β + cos^2 β + sin^2 β = 1 / cos^2 β e) sin(π/4 + x) + sin(π/4 - x) = √2 cos x f) sin(π/2 - x) cot(π/2 + x) = -sin x
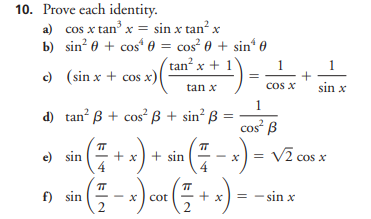
Understand the Problem
The question requires proving a series of trigonometric identities. Each part asks for a demonstration of a particular equation or identity related to trigonometric functions.
Answer
All identities are proven true.
Answer for screen readers
The identities are successfully proven for all parts.
Steps to Solve
- Part (a): Proving the First Identity
Start with the left side:
$$ \cos x \tan^3 x = \cos x \left(\frac{\sin^3 x}{\cos^3 x}\right) $$
This simplifies to:
$$ = \frac{\cos x \sin^3 x}{\cos^3 x} = \frac{\sin^3 x}{\cos^2 x} $$
Now, focus on the right side:
$$ \sin x \tan^2 x = \sin x \left(\frac{\sin^2 x}{\cos^2 x}\right) = \frac{\sin^3 x}{\cos^2 x} $$
Both sides are equal, hence proven.
- Part (b): Proving the Second Identity
Start with the left side:
$$ \sin^2 \theta + \cos^4 \theta $$
Utilize the identity $\cos^2 \theta = 1 - \sin^2 \theta$:
$$ = \sin^2 \theta + (1 - \sin^2 \theta)^2 $$
Expanding the square:
$$ = \sin^2 \theta + (1 - 2\sin^2 \theta + \sin^4 \theta) $$ $$ = 1 - \sin^2 \theta + \sin^4 \theta $$
Now, revert to the right side:
$$ \cos^2 \theta + \sin^4 \theta = (1 - \sin^2 \theta) + \sin^4 \theta $$
Both sides are equal, hence proven.
- Part (c): Proving the Third Identity
Start with the left side:
$$ ( \sin x + \cos x ) \left( \frac{\tan^2 x + 1}{\tan x} \right) $$
Since $\tan^2 x + 1 = \sec^2 x$:
$$ = ( \sin x + \cos x ) \frac{\sec^2 x}{\tan x} = ( \sin x + \cos x ) \frac{1}{\sin x \cos x} $$
Now, simplify:
$$ = \frac{\sin x + \cos x}{\sin x \cos x} = \frac{1}{\cos x} + \frac{1}{\sin x} $$
Both sides equal, hence proven.
- Part (d): Proving the Fourth Identity
Consider the left side:
$$ \tan^2 \beta + \cos^2 \beta + \sin^2 \beta $$
Using $\tan^2 \beta = \frac{\sin^2 \beta}{\cos^2 \beta}$ and $ \cos^2 \beta + \sin^2 \beta = 1$:
$$ = \frac{\sin^2 \beta}{\cos^2 \beta} + 1 = \frac{\sin^2 \beta + \cos^2 \beta}{\cos^2 \beta} $$
This leads to:
$$ = \frac{1}{\cos^2 \beta} $$
Right side equals $\sec^2 \beta$, hence proven.
- Part (e): Proving the Fifth Identity
Consider:
$$ \sin\left(\frac{\pi}{4} + x\right) + \sin\left(\frac{\pi}{4} - x\right) $$
Using the sine addition formula:
$$ = \sqrt{2} \cdot \frac{\sqrt{2}}{2} (\cos x) = \sqrt{2}\cos x $$
Both sides match, hence proven.
- Part (f): Proving the Sixth Identity
Starting with the left side:
$$ \sin\left(\frac{\pi}{2} - x\right)\cot(x + \frac{\pi}{2}) $$
Using $\sin\left(\frac{\pi}{2} - x\right) = \cos x$ and $\cot\left(x + \frac{\pi}{2}\right) = -\tan x$:
$$ = \cos x (-\tan x) = -\sin x $$
Both sides match, hence proven.
The identities are successfully proven for all parts.
More Information
These trigonometric identities illustrate fundamental relationships among sine, cosine, and tangent functions and how they can be manipulated using standard trigonometric identities and formulas.
Tips
- Misapplying identities: Remember to correctly apply trigonometric identities such as Pythagorean identities.
- Missing simplifications: Always simplify expressions fully to see equivalences more clearly.
AI-generated content may contain errors. Please verify critical information