Now, use implicit differentiation to differentiate y = (3√t)^t with respect to t, treating y as a differentiable function of t.
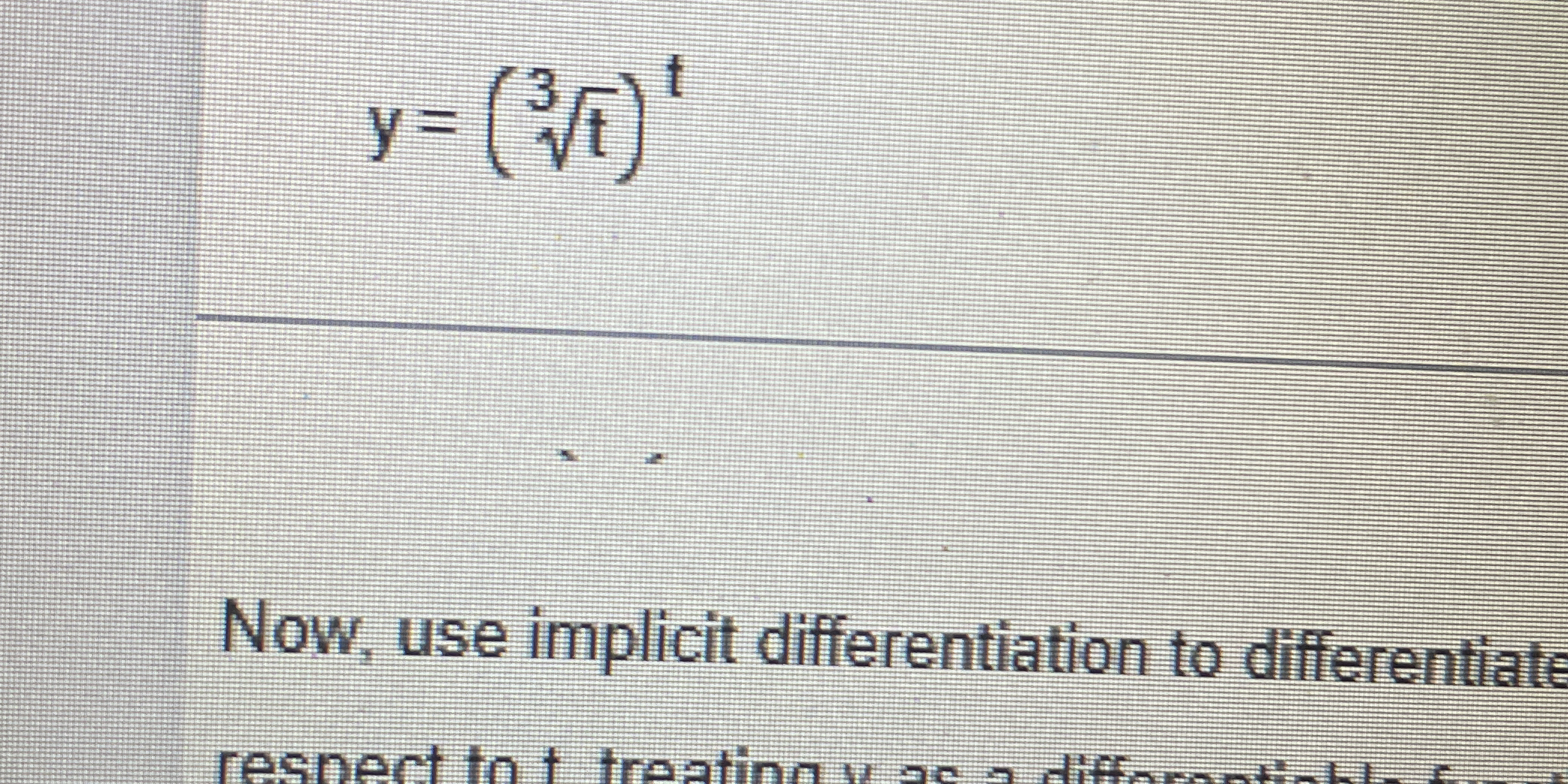
Understand the Problem
The question is asking to use implicit differentiation on the given equation where y is defined in terms of t. We will differentiate both sides of the equation with respect to t, treating y as a differentiable function of t.
Answer
$$ \frac{dy}{dt} = (3\sqrt{t})^t \left( \ln(3\sqrt{t}) + \frac{1}{2} \right) $$
Answer for screen readers
The derivative is
$$ \frac{dy}{dt} = (3\sqrt{t})^t \left( \ln(3\sqrt{t}) + \frac{1}{2} \right) $$
Steps to Solve
- Identify the equation We start with the equation given:
$$ y = (3\sqrt{t})^t $$
- Take the natural logarithm of both sides Using logarithmic differentiation, we take the natural log of both sides to simplify.
$$ \ln(y) = \ln((3\sqrt{t})^t) $$
Using the property of logarithms, we can bring down the exponent:
$$ \ln(y) = t \cdot \ln(3\sqrt{t}) $$
- Differentiate both sides with respect to ( t ) Now we differentiate both sides. Remember that when differentiating ( y ), we apply the chain rule, giving us:
$$ \frac{1}{y} \frac{dy}{dt} = \frac{d}{dt}(t \cdot \ln(3\sqrt{t})) $$
- Differentiate the right side We apply the product rule on the right side:
$$ \frac{d}{dt}(t \cdot \ln(3\sqrt{t})) = \frac{d}{dt}(t) \cdot \ln(3\sqrt{t}) + t \cdot \frac{d}{dt}(\ln(3\sqrt{t})) $$
The derivative of ( t ) is ( 1 ), and we need to find the derivative of ( \ln(3\sqrt{t}) ):
- Differentiate ( \ln(3\sqrt{t}) ) Using the properties of logarithms:
$$ \ln(3\sqrt{t}) = \ln(3) + \frac{1}{2} \ln(t) $$
Thus,
$$ \frac{d}{dt}(\ln(3\sqrt{t})) = 0 + \frac{1}{2} \cdot \frac{1}{t} = \frac{1}{2t} $$
- Combine results So, we have:
$$ \frac{1}{y} \frac{dy}{dt} = \ln(3\sqrt{t}) + t \cdot \frac{1}{2t} $$
This simplifies to:
$$ \frac{1}{y} \frac{dy}{dt} = \ln(3\sqrt{t}) + \frac{1}{2} $$
- Solve for ( \frac{dy}{dt} ) Multiply both sides by ( y ):
$$ \frac{dy}{dt} = y \left( \ln(3\sqrt{t}) + \frac{1}{2} \right) $$
Finally, substitute back ( y = (3\sqrt{t})^t ):
$$ \frac{dy}{dt} = (3\sqrt{t})^t \left( \ln(3\sqrt{t}) + \frac{1}{2} \right) $$
The derivative is
$$ \frac{dy}{dt} = (3\sqrt{t})^t \left( \ln(3\sqrt{t}) + \frac{1}{2} \right) $$
More Information
This method of using implicit differentiation and logarithmic properties simplifies the differentiation process, especially when dealing with functions with variables in both the base and exponent.
Tips
- Forgetting to apply the chain rule when differentiating ( y ).
- Not simplifying the logarithm before differentiation.
- Misapplying the product rule.
AI-generated content may contain errors. Please verify critical information