n/9 + 4 < 3
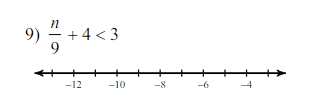
Understand the Problem
The question is asking to solve the inequality involving a variable n, specifically the inequality n/9 + 4 < 3. We will isolate n and determine the solution set.
Answer
$n < -9$
Answer for screen readers
The solution to the inequality is $n < -9$.
Steps to Solve
-
Isolate the fraction
To isolate the term with $n$, subtract 4 from both sides of the inequality: $$ \frac{n}{9} + 4 - 4 < 3 - 4 $$
This simplifies to: $$ \frac{n}{9} < -1 $$ -
Eliminate the fraction
Next, multiply both sides of the inequality by 9 to eliminate the fraction. Remember to maintain the direction of the inequality since we are multiplying by a positive number: $$ n < -1 \times 9 $$
This results in: $$ n < -9 $$ -
Graph the solution
The solution $n < -9$ can be represented on a number line. You would draw a number line and shade all values to the left of -9, indicating that all these values satisfy the inequality.
The solution to the inequality is $n < -9$.
More Information
This inequality means that $n$ can take any value less than -9. For example, -10, -11, or -20 are all valid solutions. Inequalities like this are useful in many fields, including physics and economics, where determining ranges can be critical.
Tips
-
Neglecting to change the inequality when multiplying/dividing by a negative number.
This isn't an issue here since we only multiplied by a positive number, but it's important to remember in other contexts.
AI-generated content may contain errors. Please verify critical information