List the elements of (a) A' ∩ B, (b) (A' ∩ B).
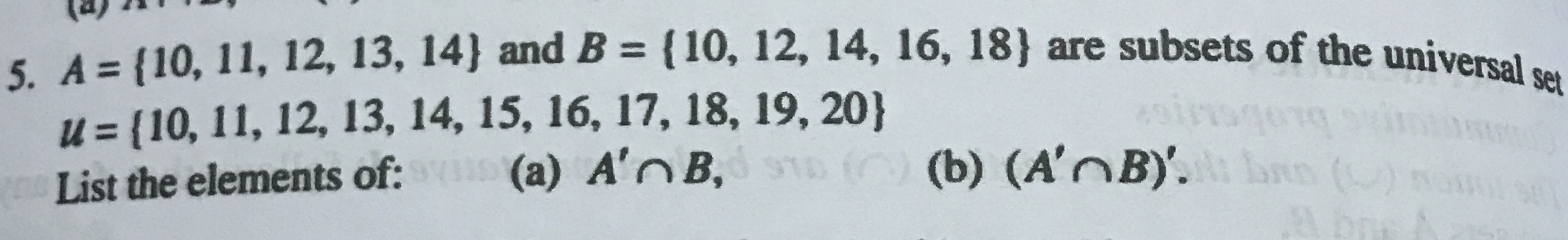
Understand the Problem
The question is asking for the elements of the intersection of the complement of set A with set B and the intersection of the complement of set A with set B, specifically the two parts (a) and (b).
Answer
\( A' \cap B = \{16, 18\} \)
Answer for screen readers
-
(a) ( A' \cap B = {16, 18} )
-
(b) ( A' \cap B = {16, 18} )
Steps to Solve
- Determine the complement of set A
The complement of set A, denoted as ( A' ), includes all elements in the universal set ( U ) that are not in ( A ).
$$ A' = U \setminus A = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20} \setminus {10, 11, 12, 13, 14} = {15, 16, 17, 18, 19, 20} $$
- Find the intersection of ( A' ) and set B
Now we will find the intersection of ( A' ) and B, denoted as ( A' \cap B ). The intersection includes elements that are present in both sets.
$$ A' \cap B = {15, 16, 17, 18, 19, 20} \cap {10, 12, 14, 16, 18} = {16, 18} $$
- Determine the elements for part (a)
For part (a), we have:
$$ A' \cap B = {16, 18} $$
- Find the intersection of ( A' ) and ( B ) for part (b)
Since part (b) is the same as part (a), we have:
$$ A' \cap B = {16, 18} $$
-
(a) ( A' \cap B = {16, 18} )
-
(b) ( A' \cap B = {16, 18} )
More Information
The complement of a set consists of all items not in that set, based on the universal set. The intersection finds common elements between two sets, highlighting shared members.
Tips
- Ignoring the Universal Set: Make sure to reference the correct universal set when finding complements.
- Confusing Complement with Intersection: Remember that the complement excludes elements from the original set, while the intersection is about finding shared elements.
AI-generated content may contain errors. Please verify critical information