What is the value of x in -x = \frac{9}{7} - \frac{2}{3}?
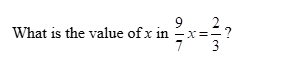
Understand the Problem
The question is asking to find the value of x in the equation where -x is equal to a fraction derived from the equations provided.
Answer
The value of \( x \) is \( -\frac{13}{21} \).
Answer for screen readers
The value of ( x ) is ( -\frac{13}{21} ).
Steps to Solve
- Simplify the Right Side of the Equation
First, compute the right side of the equation by finding a common denominator for the fractions $\frac{9}{7}$ and $\frac{2}{3}$. The least common multiple of 7 and 3 is 21.
To convert the fractions: $$ \frac{9}{7} = \frac{9 \times 3}{7 \times 3} = \frac{27}{21} $$ $$ \frac{2}{3} = \frac{2 \times 7}{3 \times 7} = \frac{14}{21} $$
Now, substitute these back into the equation: $$ -x = \frac{27}{21} - \frac{14}{21} $$
- Perform the Subtraction of Fractions
Now, simplify the right side: $$ -x = \frac{27 - 14}{21} $$
Calculate the numerator: $$ -x = \frac{13}{21} $$
- Isolate x
Next, to find $x$, multiply both sides by -1: $$ x = -\frac{13}{21} $$
The value of ( x ) is ( -\frac{13}{21} ).
More Information
This problem demonstrates the process of solving a simple algebraic equation with fractions. Knowing how to find a common denominator is a useful skill when working with fractions. The negative sign indicates that the value is less than zero.
Tips
- Failing to find a common denominator when subtracting fractions.
- Forgetting to multiply by -1 when isolating ( x ).
AI-generated content may contain errors. Please verify critical information