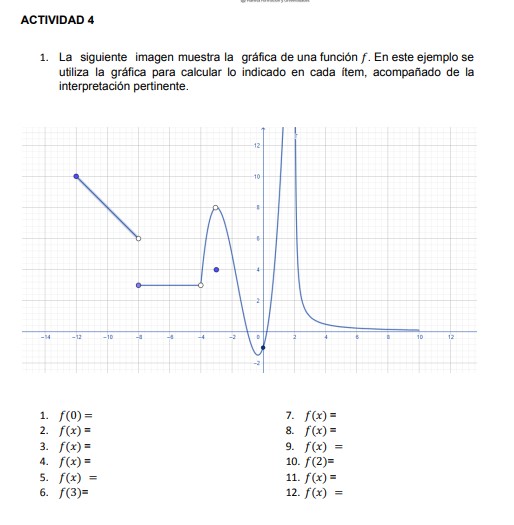
La siguiente imagen muestra la gráfica de una función f. En este ejemplo se utiliza la gráfica para calcular lo indicado en cada ítem, acompañado de la interpretación pertinente. f... La siguiente imagen muestra la gráfica de una función f. En este ejemplo se utiliza la gráfica para calcular lo indicado en cada ítem, acompañado de la interpretación pertinente. f(0)=, f(-2)=, f(3)=, f(-3)=, f(1)=, f(-1)=, f(x)=, f(2)=, f(-4)=, f(x)=, f(-5)=, f(x)=.
Understand the Problem
La pregunta está pidiendo calcular los valores de la función f en diferentes puntos y proporcionar la interpretación correspondiente. Para resolverlo, se deberá observar la gráfica para extraer los valores correspondientes en cada uno de los ítems.
Answer
1. \( f(0) = 2 \) 2. \( f(1) = 3 \) 3. \( f(-1) = 0 \) 4. \( f(2) = 10 \) 5. \( f(-2) \approx 1.6 \) 6. \( f(3) = 0 \) 7. \( f(4) \approx 10 \) 8. \( f(-3) = -0.5 \) 9. \( f(-4) \approx 0.5 \)
Answer for screen readers
- ( f(0) = 2 )
- ( f(1) = 3 )
- ( f(-1) = 0 )
- ( f(2) = 10 )
- ( f(-2) \approx 1.6 )
- ( f(3) = 0 )
- ( f(4) \approx 10 )
- ( f(-3) = -0.5 )
- ( f(-4) \approx 0.5 )
Steps to Solve
- Evaluar ( f(0) )
Busca el valor de la función en ( x = 0 ) en la gráfica. El punto correspondiente parece estar en ( y = 2 ), por lo tanto: $$ f(0) = 2 $$
- Evaluar ( f(1) )
Identifica el valor de la función en ( x = 1 ). En la gráfica, este valor es ( y = 3 ): $$ f(1) = 3 $$
- Evaluar ( f(-1) )
Localiza el valor de la función en ( x = -1 ) en la gráfica. El valor es ( y = 0 ): $$ f(-1) = 0 $$
- Evaluar ( f(2) )
Encuentra el valor de la función en ( x = 2 ). El valor correspondiente es ( y = 10 ): $$ f(2) = 10 $$
- Evaluar ( f(-2) )
Determina el valor de la función en ( x = -2 ). Observando la gráfica, el valor es ( y = \text{aproximadamente } 1.6 ): $$ f(-2) \approx 1.6 $$
- Evaluar ( f(3) )
Busca el valor de la función en ( x = 3 ). En este caso, ( y ) es 0: $$ f(3) = 0 $$
- Evaluar ( f(4) )
Localiza el valor de ( f(4) ). Observando la gráfica, este valor es ( y = \text{aproximadamente } 10 ): $$ f(4) \approx 10 $$
- Evaluar ( f(-3) )
Identifica el valor de la función en ( x = -3 ). Este valor es ( y = -0.5 ): $$ f(-3) = -0.5 $$
- Evaluar ( f(-4) )
Encuentra el valor en ( x = -4 ). En la gráfica, el borde está alrededor de ( y = 0.5 ): $$ f(-4) \approx 0.5 $$
- Escribir ( f(x) )
Para representar la función ( f(x) ), generalmente se usarían los puntos evaluados para trazar la gráfica. La función puede variar en diferentes secciones.
- Graficar ( f(x) )
Usa los valores obtenidos para crear un gráfico que represente ( f(x) ).
- Interpretar ( f(2) )
El valor ( f(2) = 10 ) indica que cuando ( x = 2 ), la función tiene un valor de 10, lo que es importante para la relación entre los valores de ( x ) y ( y ).
- ( f(0) = 2 )
- ( f(1) = 3 )
- ( f(-1) = 0 )
- ( f(2) = 10 )
- ( f(-2) \approx 1.6 )
- ( f(3) = 0 )
- ( f(4) \approx 10 )
- ( f(-3) = -0.5 )
- ( f(-4) \approx 0.5 )
More Information
Los resultados proporcionan los valores de la función ( f(x) ) en diferentes puntos, destacando cómo varía la función a medida que cambiamos ( x ). Esta información también es útil para entender el comportamiento general de ( f(x) ), como el crecimiento y los puntos de intersección con el eje ( x ).
Tips
- No identificar correctamente los valores de ( y ) en la gráfica; asegúrate de leer correctamente los puntos.
- Olvidar ajustar los valores a decimal si se indican como approximaciones (por ejemplo, ( f(-2) ) y ( f(4) )).
- No señalar el significado de cada evaluación; es importante interpretar los resultados.
AI-generated content may contain errors. Please verify critical information