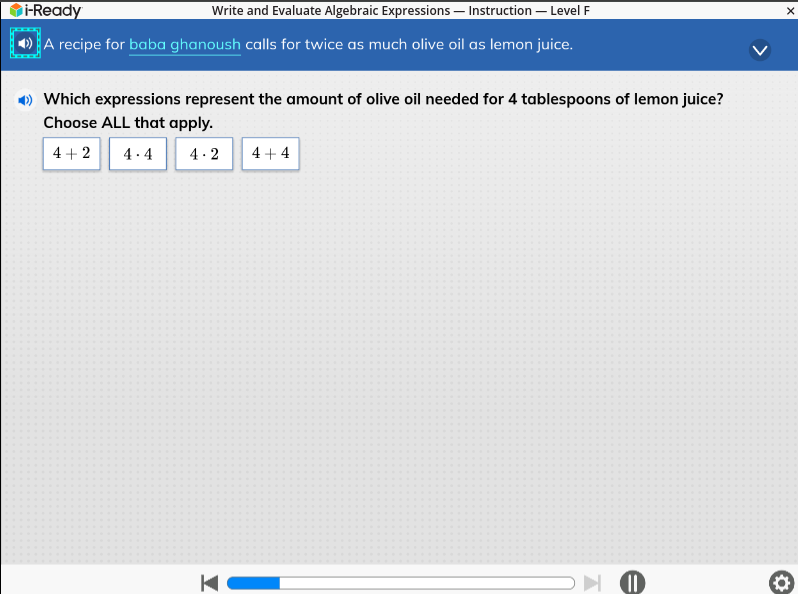
Which expressions represent the amount of olive oil needed for 4 tablespoons of lemon juice? Choose ALL that apply.

Understand the Problem

The question is asking for algebraic expressions that represent the amount of olive oil needed for a recipe calling for twice as much olive oil as lemon juice. Specifically, it involves calculating the amount of olive oil required based on a given quantity of lemon juice (4 tablespoons).

Answer

The valid expressions are $4 \times 2$ and $4 + 4$.

Steps to Solve

Identify the required amount of olive oil
The recipe states that the amount of olive oil needs to be twice as much as the amount of lemon juice. Given that the recipe calls for 4 tablespoons of lemon juice, we can express the amount of olive oil as:
$$ \text{Olive Oil} = 2 \times \text{Lemon Juice} = 2 \times 4 $$
Calculate the value of olive oil
Now, we perform the multiplication:
$$ \text{Olive Oil} = 2 \times 4 = 8 $$
So, 8 tablespoons of olive oil are needed.
Evaluate the expressions
Next, we will evaluate each expression given in the options to see which equals 8 tablespoons:

$4 + 2 = 6$
$4 \times 4 = 16$
$4 \times 2 = 8$
$4 + 4 = 8$

Select the correct expressions
From the evaluation, we note that the expressions that represent the amount of olive oil needed are:

$4 \times 2 = 8$
$4 + 4 = 8$

The expressions that represent the amount of olive oil needed are:

$4 \times 2$
$4 + 4$

More Information

The recipe requires twice the amount of olive oil compared to lemon juice. In this case, since 4 tablespoons of lemon juice are used, it results in needing 8 tablespoons of olive oil. The expressions that equal 8 are valid for this calculation.

Tips

Confusing addition and multiplication: Some might mistakenly add instead of multiplying when determining the relationship between olive oil and lemon juice.
Not recognizing 'twice as much' implies multiplication by 2.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!