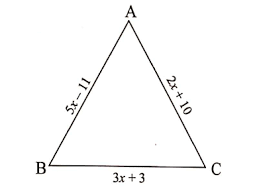
In the triangle ABC, side AB is 5x - 11, side AC is 2x + 10, and side BC is 3x + 3. What is the value of x?

Understand the Problem

The question presents a triangle with sides represented as algebraic expressions and likely requires finding the value of 'x' by using the property that the sum of angles in a triangle is 180 degrees or solving for the lengths of sides under given conditions.

Answer

The condition for $ x $ is $ x > 3 $.

Steps to Solve

Assign the sides of the triangle Let the sides of triangle ABC be defined as follows:

Side AB: ( 5x - 11 )
Side AC: ( 2x + 10 )
Side BC: ( 3x + 3 )

Use the triangle inequality theorem According to the triangle inequality theorem, the sum of the lengths of any two sides must be greater than the length of the third side. We will set up three inequalities:

Inequality 1: ( (5x - 11) + (2x + 10) > (3x + 3) )

Simplifying: $$ 7x - 1 > 3x + 3 $$ $$ 4x > 4 $$ $$ x > 1 $$

Inequality 2: ( (5x - 11) + (3x + 3) > (2x + 10) )

Simplifying: $$ 8x - 8 > 2x + 10 $$ $$ 6x > 18 $$ $$ x > 3 $$

Inequality 3: ( (2x + 10) + (3x + 3) > (5x - 11) )

Simplifying: $$ 5x + 13 > 5x - 11 $$ This inequality is always true.

Combine the inequalities From the first two inequalities, we can deduce that ( x > 3 ) is the strongest condition since both inequalities need to be satisfied.
Conclusion Since the only valid condition is ( x > 3 ), we can conclude that this is the required condition for the sides of the triangle.

The condition for ( x ) is ( x > 3 ).

More Information

This condition ensures that the sides of triangle ABC adhere to the triangle inequality theorem, confirming that they can exist as the lengths of a triangle.

Tips

Ignoring one of the triangle inequalities can lead to incorrect conclusions. Always check all three inequalities to ensure that all conditions are satisfied for a valid triangle.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!