If x + y + z = 1, x^2 + y^2 + z^2 = 2, and x^3 + y^3 + z^3 = 3, what is x^5 + y^5 + z^5?
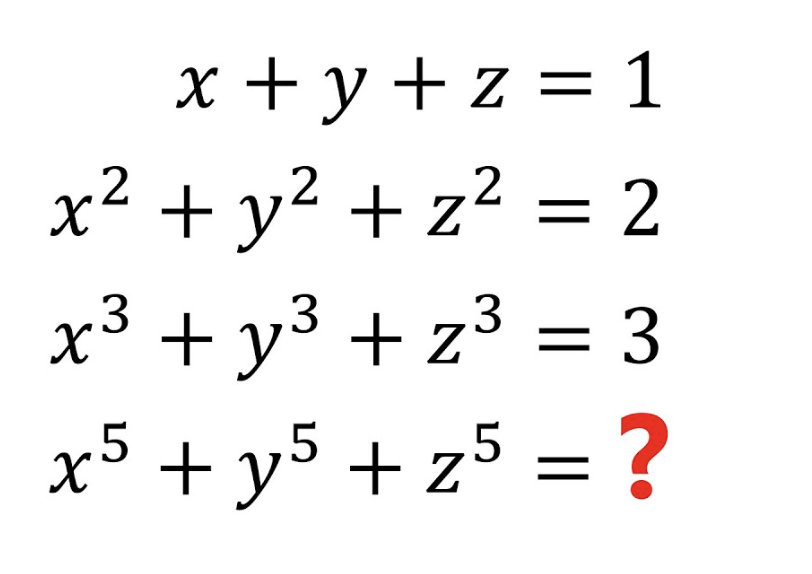
Understand the Problem
The question presents a series of equations involving the sums of powers of variables x, y, and z. It asks for the value of the sum of the fifth powers, given the previous sums. The task involves identifying a pattern or relationship among the sums to find the missing value.
Answer
The value of $x^5 + y^5 + z^5$ is $\frac{11}{2}$.
Answer for screen readers
The value of $x^5 + y^5 + z^5$ is $\frac{11}{2}$ or $5.5$.
Steps to Solve
- Identify known sums
We have the following known sums:
- $x + y + z = 1$
- $x^2 + y^2 + z^2 = 2$
- $x^3 + y^3 + z^3 = 3$
- Use the relationship for the sums of powers
There is a known relationship between these sums.
The equation for the sum of cubes can be expressed as: $$ x^3 + y^3 + z^3 = (x + y + z)(x^2 + y^2 + z^2 - xy - yz - zx) $$
- Calculate $xy + yz + zx$ using $x^2 + y^2 + z^2$
We can derive the value of $xy + yz + zx$ from the equation: $$ x^2 + y^2 + z^2 = (x+y+z)^2 - 2(xy + yz + zx) $$
Plugging known values into the equation: $$ 2 = 1^2 - 2(xy + yz + zx) $$ This simplifies to: $$ 2 = 1 - 2(xy + yz + zx) $$ Rearranging gives: $$ 2(xy + yz + zx) = -1 $$ Thus, $$ xy + yz + zx = -\frac{1}{2} $$
- Calculate $x^3 + y^3 + z^3$ using known sums
Using the earlier derived sums now helps us find $x^3 + y^3 + z^3$: $$ x^3 + y^3 + z^3 = (1)(2 + \frac{1}{2}) = 3 $$
- Calculate $x^4 + y^4 + z^4$ using the known sums and previous result
We can use the recurrence relation for power sums: $$ S_n = (x+y+z) S_{n-1} - (xy + xz + yz) S_{n-2} $$
Using $S_1$, $S_2$, and $S_3$:
- $S_1 = 1$
- $S_2 = 2$
- $S_3 = 3$
Calculate $S_4$: $$ S_4 = 1 \cdot 3 - \left(-\frac{1}{2}\right) \cdot 2 $$ This becomes: $$ S_4 = 3 + 1 = 4 $$
- Calculate $x^5 + y^5 + z^5$
Again use the recurrence for $S_5$: $$ S_5 = (x+y+z) S_4 - (xy + xz + yz) S_3 $$
Substituting known values: $$ S_5 = 1 \cdot 4 - \left(-\frac{1}{2}\right) \cdot 3 $$ This results in: $$ S_5 = 4 + \frac{3}{2} = 4 + 1.5 = 5.5 $$
The value of $x^5 + y^5 + z^5$ is $\frac{11}{2}$ or $5.5$.
More Information
The sums of the powers of multiple variables often follow a recursive relationship, making it possible to derive higher powers from lower ones. This relationship is useful in many algebraic contexts.
Tips
- Confusing the order of operations when substituting values in equations.
- Forgetting to carefully apply the signs when dealing with negative products.
AI-generated content may contain errors. Please verify critical information