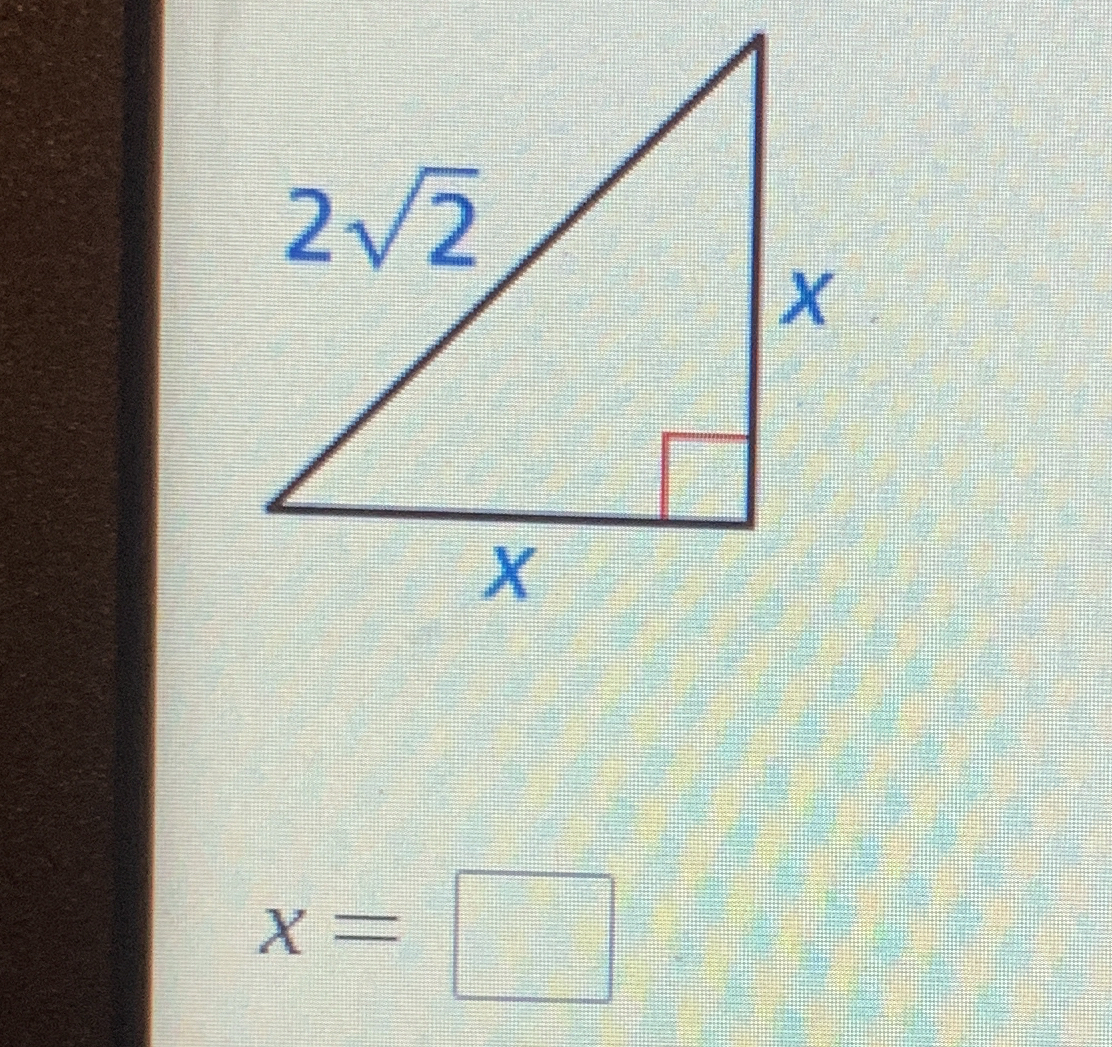
In a right triangle, if one side is 2√2 and the other two sides are x, find x.
Understand the Problem
The question is asking to determine the value of 'x' in a right triangle where one side is '2√2' and the other two sides are both 'x'. This involves using the Pythagorean theorem.
Answer
$x = 2$
Answer for screen readers
$x = 2$
Steps to Solve
-
Identify the sides of the triangle In this right triangle, we have two equal sides of length $x$ and one side of length $2\sqrt{2}$.
-
Apply the Pythagorean theorem The Pythagorean theorem states that in a right triangle, the sum of the squares of the legs equals the square of the hypotenuse. Here, we can express this as: $$ x^2 + x^2 = (2\sqrt{2})^2 $$
-
Simplify the equation Combine the terms on the left side and simplify the right side: $$ 2x^2 = (2\sqrt{2})^2 $$ Calculating the right side gives: $$ (2\sqrt{2})^2 = 4 \cdot 2 = 8 $$
-
Set up the equation Now we have: $$ 2x^2 = 8 $$
-
Solve for x Divide both sides by 2: $$ x^2 = 4 $$ Taking the square root of both sides, we find: $$ x = 2 $$
$x = 2$
More Information
In a right triangle with two equal sides, known as an isosceles right triangle, the sides opposite the 45-degree angles both measure the same length. In this case, both sides measure 2.
Tips
- Forgetting to square the hypotenuse correctly.
- Confusing the lengths of the sides or not applying the Pythagorean theorem correctly.
AI-generated content may contain errors. Please verify critical information