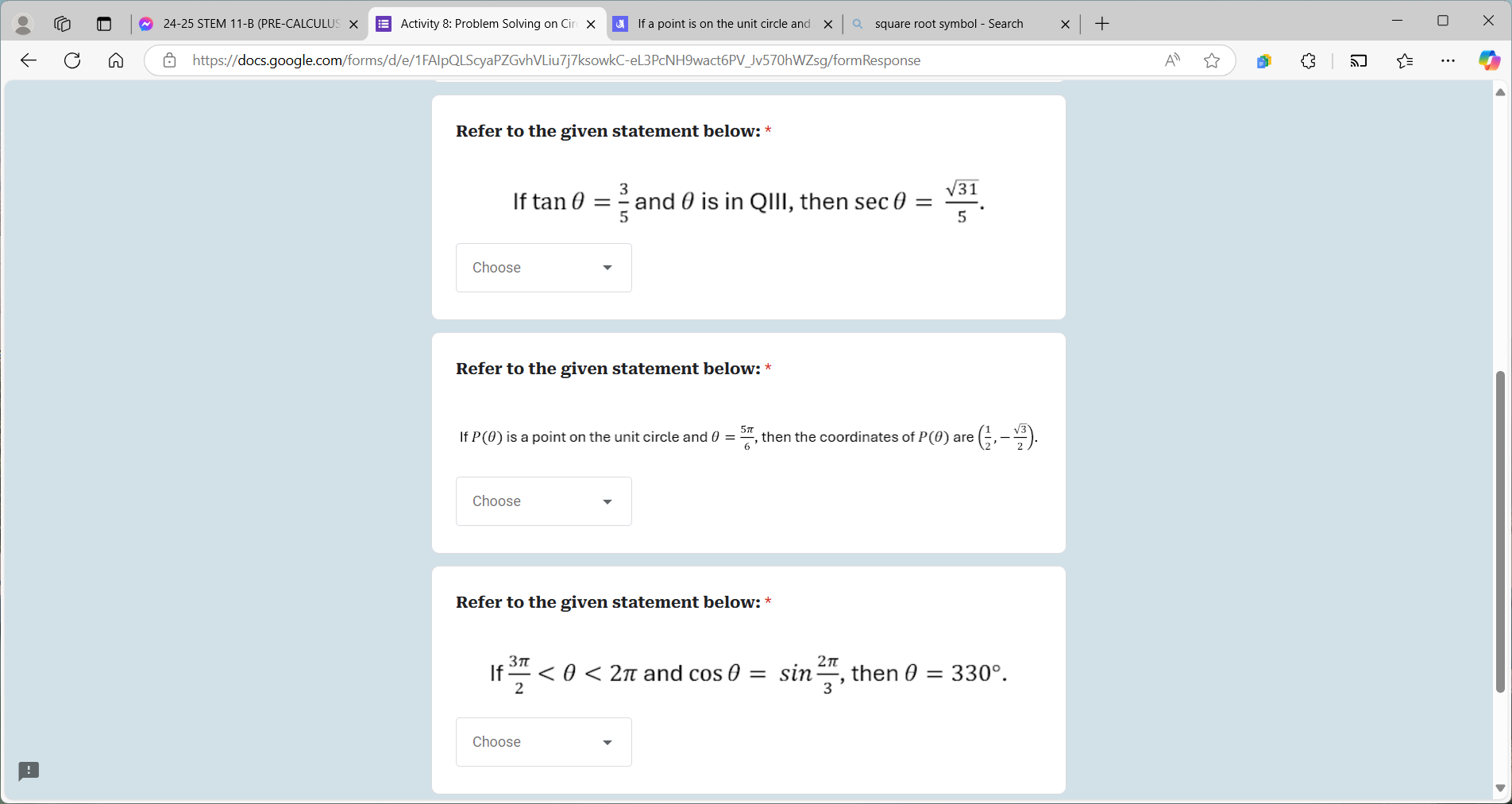
If tan θ = 3/5 and θ is in QIII, then sec θ = √31/5. If P(θ) is a point on the unit circle and θ = 5π/6, then the coordinates of P(θ) are (1/2, -√3/2). If 3π/2 < θ < 2π and cos θ =... If tan θ = 3/5 and θ is in QIII, then sec θ = √31/5. If P(θ) is a point on the unit circle and θ = 5π/6, then the coordinates of P(θ) are (1/2, -√3/2). If 3π/2 < θ < 2π and cos θ = sin(2π/3), then θ = 330°. Read more

Steps to Solve

1. Finding the Secant Value Using Tangent
   Given that $tan \theta = \frac{3}{5}$ and $\theta$ is in quadrant III, we can find $sec \theta$. First, we calculate the hypotenuse using the Pythagorean theorem:
   $$ r = \sqrt{(opposite)^2 + (adjacent)^2} = \sqrt{3^2 + 5^2} = \sqrt{9 + 25} = \sqrt{34} $$
   Next, the secant is defined as the reciprocal of the cosine. With adjacent side (-5) and hypotenuse $\sqrt{34}$:
   $$ sec \theta = \frac{1}{cos \theta} = \frac{r}{adjacent} = \frac{\sqrt{34}}{-5} $$

2. Identifying Coordinates on the Unit Circle
   For the angle $θ = \frac{5\pi}{6}$, we determine the coordinates of point $P(θ)$. The coordinates are given by:
   $$ \left( cos \frac{5\pi}{6}, sin \frac{5\pi}{6} \right) $$
   Evaluating these:
   $$ cos \frac{5\pi}{6} = -\frac{\sqrt{3}}{2}, \quad sin \frac{5\pi}{6} = \frac{1}{2} $$
   Thus, the coordinates are:
   $$ P(θ) = \left(-\frac{\sqrt{3}}{2}, \frac{1}{2}\right) $$

3. Solving for the Angle
   Given the conditions $ \frac{3\pi}{2} < θ < 2\pi $ and $ cos θ = sin \frac{2\pi}{3} $, we need to find $θ$. First, compute $sin \frac{2\pi}{3}$:
   $$ sin \frac{2\pi}{3} = \frac{\sqrt{3}}{2} $$
   Since $cos θ = \frac{\sqrt{3}}{2}$, we need the cosine value in the fourth quadrant. The angle corresponding to that cosine value is:
   $$ θ = 330° = \frac{11\pi}{6} $$