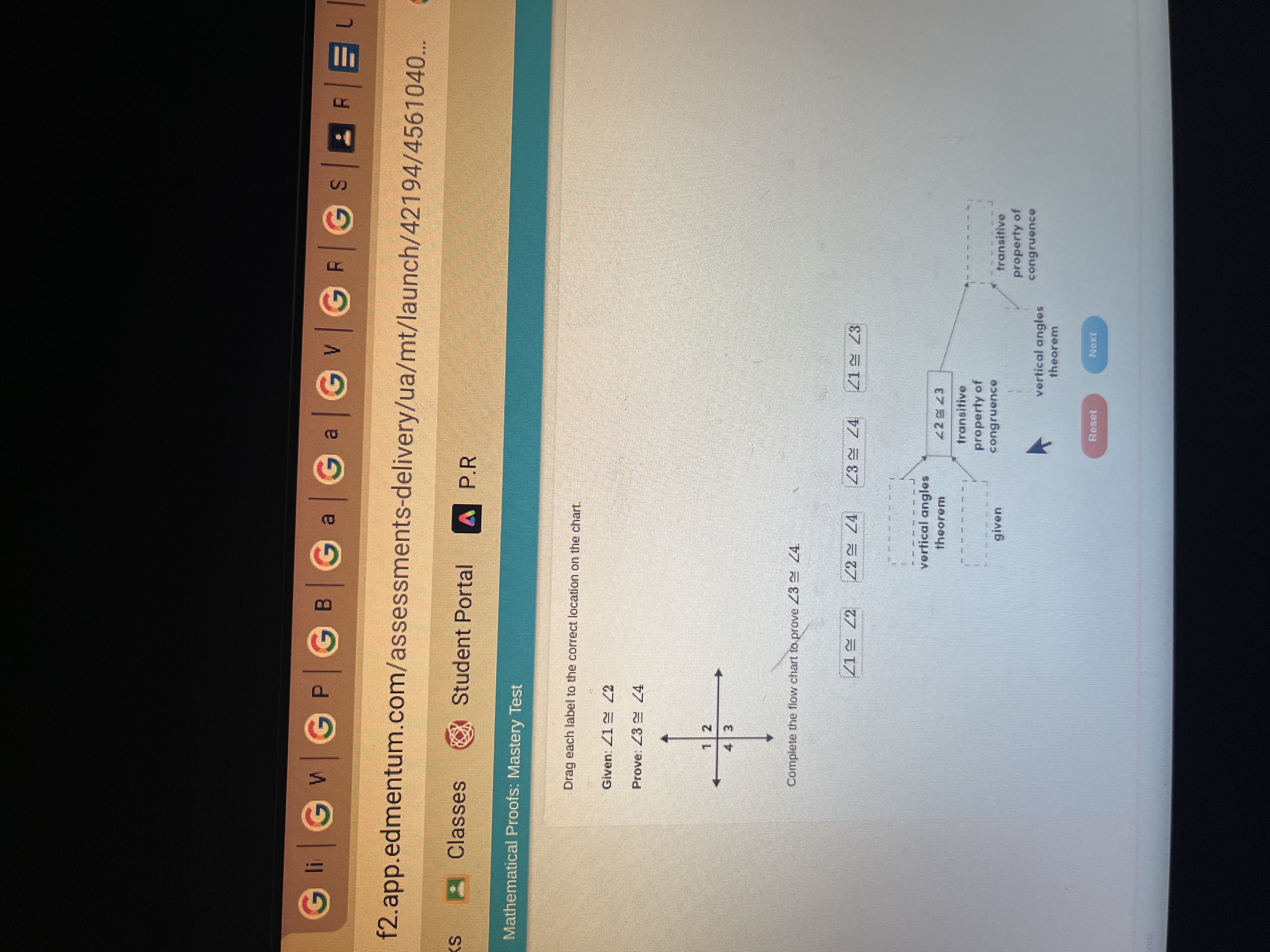
Drag each label to the correct location on the chart. Given: ∠1 ≅ ∠2 Prove: ∠3 ≅ ∠4 Complete the flow chart to prove ∠3 ≅ ∠4.
Understand the Problem
The question involves completing a flow chart to prove the congruence of angles, specifically showing how to prove that angle 3 is congruent to angle 4 using given information and properties of congruence.
Answer
$$ \angle 3 \cong \angle 4 $$
Answer for screen readers
$$ \angle 3 \cong \angle 4 $$
Steps to Solve
- Start with Given Information
The problem states that $ \angle 1 \cong \angle 2 $ is the given information.
- Apply Vertical Angles Theorem
We know that vertical angles are congruent, so we can state that:
$$ \angle 2 \cong \angle 3 $$
This is according to the Vertical Angles Theorem.
- Use Transitive Property of Congruence
Since $ \angle 1 \cong \angle 2 $ and $ \angle 2 \cong \angle 3 $, we can state that:
$$ \angle 1 \cong \angle 3 $$
This follows from the Transitive Property of Congruence.
- Again Apply Vertical Angles Theorem
Identify that:
$$ \angle 2 \cong \angle 4 $$
This again uses the Vertical Angles Theorem (assuming angles 2 and 4 are vertical).
- Conclude with Transitive Property of Congruence
Finally, since we have:
$$ \angle 1 \cong \angle 3 $$ and $$ \angle 2 \cong \angle 4 $$,
We can conclude that:
$$ \angle 3 \cong \angle 4 $$
Using the Transitive Property of Congruence one last time.
$$ \angle 3 \cong \angle 4 $$
More Information
This conclusion is based on the relationships established through the Vertical Angles Theorem and the Transitive Property of Congruence. Vertical angles are always congruent, and if two angles are each congruent to a third angle, they are congruent to each other.
Tips
- A common mistake is not recognizing the nature of vertical angles; they are always congruent.
- Another mistake is misapplying the transitive property, such as omitting one of the necessary congruences.
AI-generated content may contain errors. Please verify critical information