If l || m, solve for x and y.
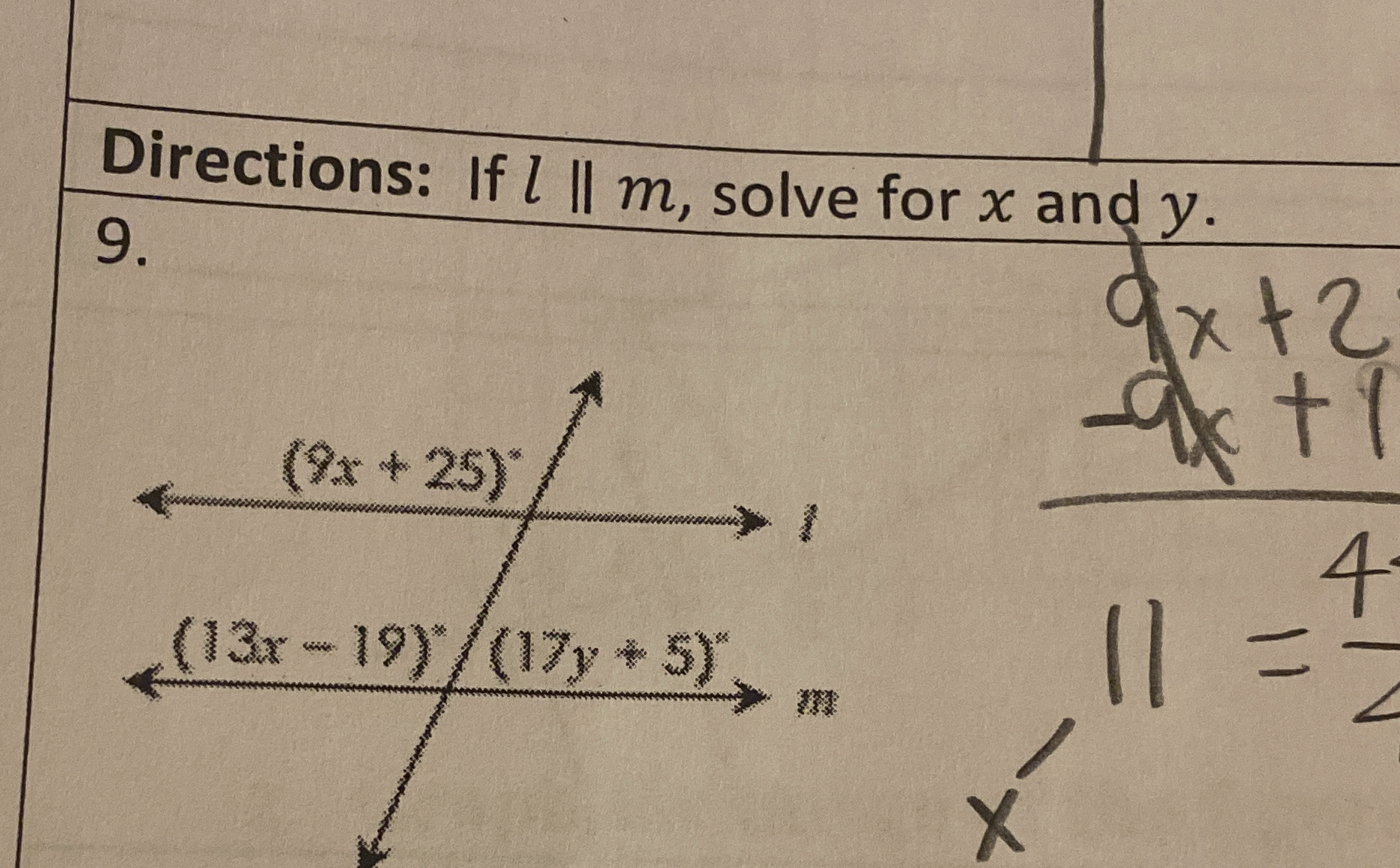
Understand the Problem
The question is asking to solve for the variables x and y given two pairs of parallel lines characterized by their angle measures. The solution involves applying properties of angles formed by parallel lines.
Answer
$x = 11$, $y \approx 7$.
Answer for screen readers
The solutions are $x = 11$ and $y \approx 7$.
Steps to Solve
- Set up equations from corresponding angles
Since $(9x + 25)^\circ$ and $(13x - 19)^\circ$ are corresponding angles, we can set them equal to each other: $$ 9x + 25 = 13x - 19 $$
- Solve for x
Rearranging the equation to isolate $x$:
- Subtract $9x$ from both sides: $$ 25 = 4x - 19 $$
- Add 19 to both sides: $$ 44 = 4x $$
- Divide by 4: $$ x = 11 $$
- Substitute x into the second set of angles
Next, use the value of $x$ to find $y$ using the angles $(17y + 5)^\circ$ and $(9x + 25)^\circ$. Substitute $x = 11$ into $(9x + 25)^\circ$: $$ 9(11) + 25 = 99 + 25 = 124 $$ Set this equal to $(17y + 5)^\circ$: $$ 17y + 5 = 124 $$
- Solve for y
Subtract 5 from both sides: $$ 17y = 119 $$ Now, divide by 17: $$ y = \frac{119}{17} \approx 7 $$
The solutions are $x = 11$ and $y \approx 7$.
More Information
This problem involves properties of parallel lines and the concept of corresponding angles, which states that when two parallel lines are crossed by a transversal, the angles in matching corners are equal. Solving for the variables involves setting up and solving linear equations.
Tips
- Incorrectly assuming angles are equal: Make sure to identify which angles are corresponding correctly.
- Arithmetic errors while solving equations: Double-check each algebraic manipulation to avoid simple mistakes.
AI-generated content may contain errors. Please verify critical information