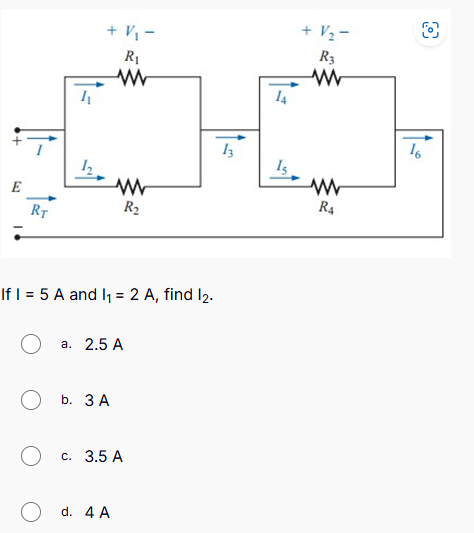
If I = 5 A and I1 = 2 A, find I2.
Understand the Problem
The question is asking to find the current I2 in an electrical circuit given specific current values. We will analyze the circuit using Kirchhoff's laws to establish the relationships between the currents and solve for I2.
Answer
$I_2 = 3 \, \text{A}$
Answer for screen readers
$I_2 = 3 , \text{A}$
Steps to Solve
- Identify given values You are given:
- Total current, $I = 5 , \text{A}$
- Current $I_1 = 2 , \text{A}$
- Apply Kirchhoff’s First Law According to Kirchhoff's Current Law (KCL), the total current entering a junction must equal the total current leaving the junction. For the junction at the left of the circuit,
$$ I = I_1 + I_2 $$
Substituting the known values,
$$ 5 = 2 + I_2 $$
- Solve for I2 Rearrange the equation to solve for $I_2$:
$$ I_2 = 5 - 2 $$
Calculating gives:
$$ I_2 = 3 , \text{A} $$
$I_2 = 3 , \text{A}$
More Information
The current $I_2$ is found using Kirchhoff's Current Law, which is essential for analyzing circuits and understanding how current divides at junctions. It helps in calculating unknown currents when other current values are known.
Tips
- Forgetting to apply KCL correctly may lead to incorrect current values. Always check that the sum of currents entering a junction matches the sum of those leaving.
- Miscalculating arithmetic might result in wrong values, so double-check your calculations.
AI-generated content may contain errors. Please verify critical information