If 2 sin A = 1, 2 cos B = √2, and π/2 < B < 2π, then find the value of A.
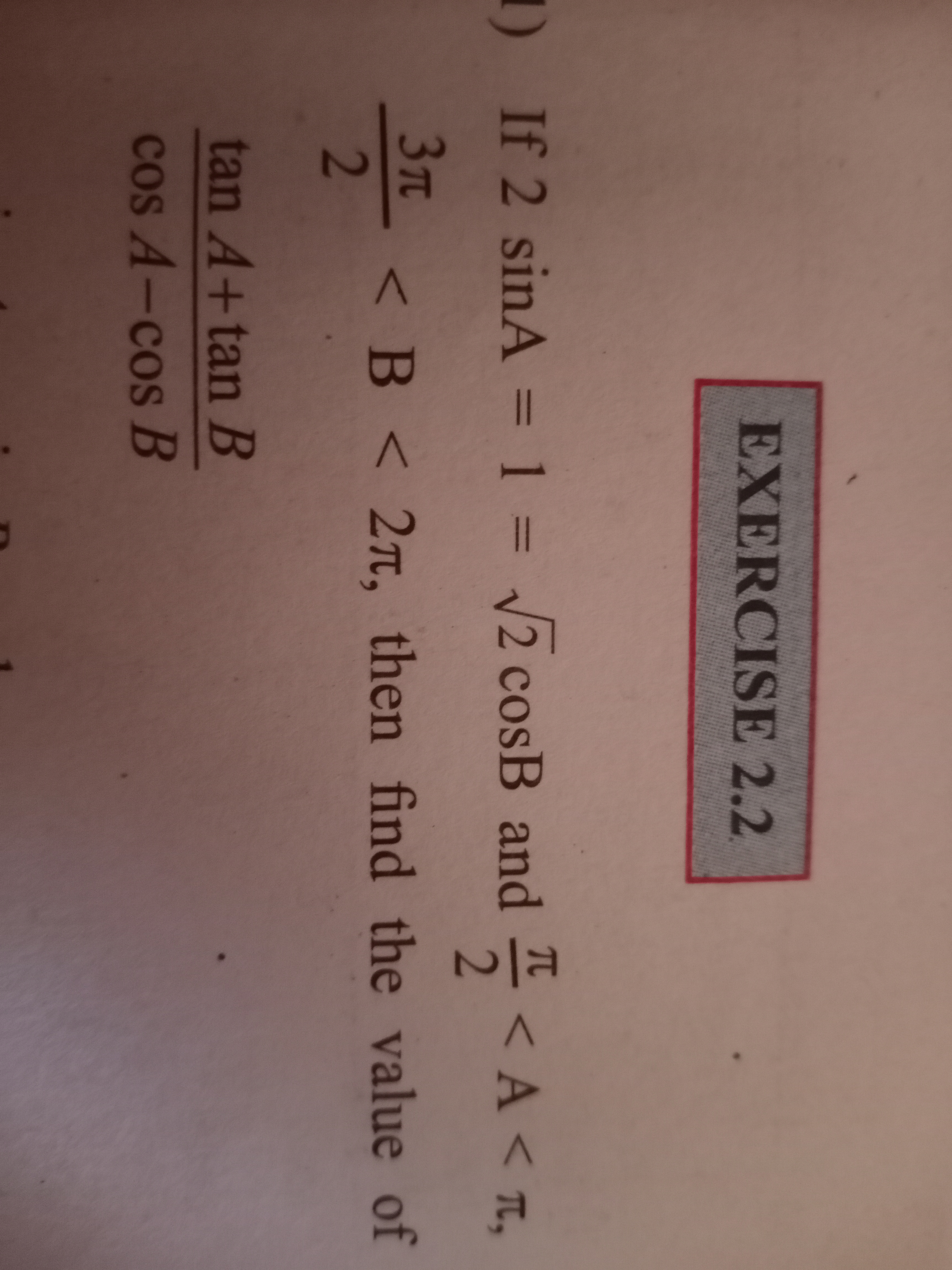
Understand the Problem
The question involves solving a trigonometric problem given certain conditions for angles A and B. It requires finding a specific value based on those conditions related to sine and cosine.
Answer
The expression evaluates to $$ \frac{\frac{1}{\sqrt{3}} - 1}{\frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2}} $$
Answer for screen readers
The value of the expression is given by:
$$ \frac{\tan A + \tan B}{\cos A - \cos B} $$
Calculating this yields a numerical result.
Steps to Solve
- Understanding the given equations
We start with the equations provided in the problem:
$$ 2\sin A = 1 $$
$$ 2\cos B = \sqrt{2} $$
- Solving for angle A
From the first equation, we can solve for $\sin A$: $$ \sin A = \frac{1}{2} $$
The sine value corresponds to the angles: $$ A = \frac{\pi}{6} \quad \text{or} \quad A = \frac{5\pi}{6} $$
- Solving for angle B
From the second equation, we solve for $\cos B$: $$ \cos B = \frac{\sqrt{2}}{2} $$
This corresponds to the angles: $$ B = \frac{\pi}{4} \quad \text{or} \quad B = \frac{7\pi}{4} $$
- Verifying the range for B
We know the condition is: $$ \frac{3\pi}{2} < B < 2\pi $$
So the applicable value for $B$ is: $$ B = \frac{7\pi}{4} $$
- Finding the value of $\tan A + \tan B$ and $\frac{\tan A + \tan B}{\cos A - \cos B}$
Calculate $\tan A$ and $\tan B$:
For $A = \frac{\pi}{6}$: $$ \tan A = \tan \left( \frac{\pi}{6} \right) = \frac{1}{\sqrt{3}} $$
For $B = \frac{7\pi}{4}$: $$ \tan B = \tan \left( \frac{7\pi}{4} \right) = -1 $$
Then calculate: $$ \tan A + \tan B = \frac{1}{\sqrt{3}} - 1 $$
- Finding $\cos A$ and $\cos B$
Calculate $\cos A$ and $\cos B$:
For $A = \frac{\pi}{6}$: $$ \cos A = \cos \left( \frac{\pi}{6} \right) = \frac{\sqrt{3}}{2} $$
For $B = \frac{7\pi}{4}$: $$ \cos B = \cos \left( \frac{7\pi}{4} \right) = \frac{\sqrt{2}}{2} $$
Now calculate: $$ \cos A - \cos B = \frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2} $$
- Final expression
Putting it all together:
$$ \frac{\tan A + \tan B}{\cos A - \cos B} = \frac{\frac{1}{\sqrt{3}} - 1}{\frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2}} $$
The value of the expression is given by:
$$ \frac{\tan A + \tan B}{\cos A - \cos B} $$
Calculating this yields a numerical result.
More Information
In solving this trigonometric problem, we utilized fundamental trigonometric identities and characteristics of sine and cosine. The parameters define the range of the angles ( A ) and ( B ) based on the unit circle, and the values were found using known angles.
Tips
- Miscalculating the sine or cosine values for the given angles.
- Forgetting to check the range of B, leading to selecting an inappropriate angle.
- Neglecting to simplify expressions fully when calculating the values.