Simplify log_c b × log_a c × log_b a.
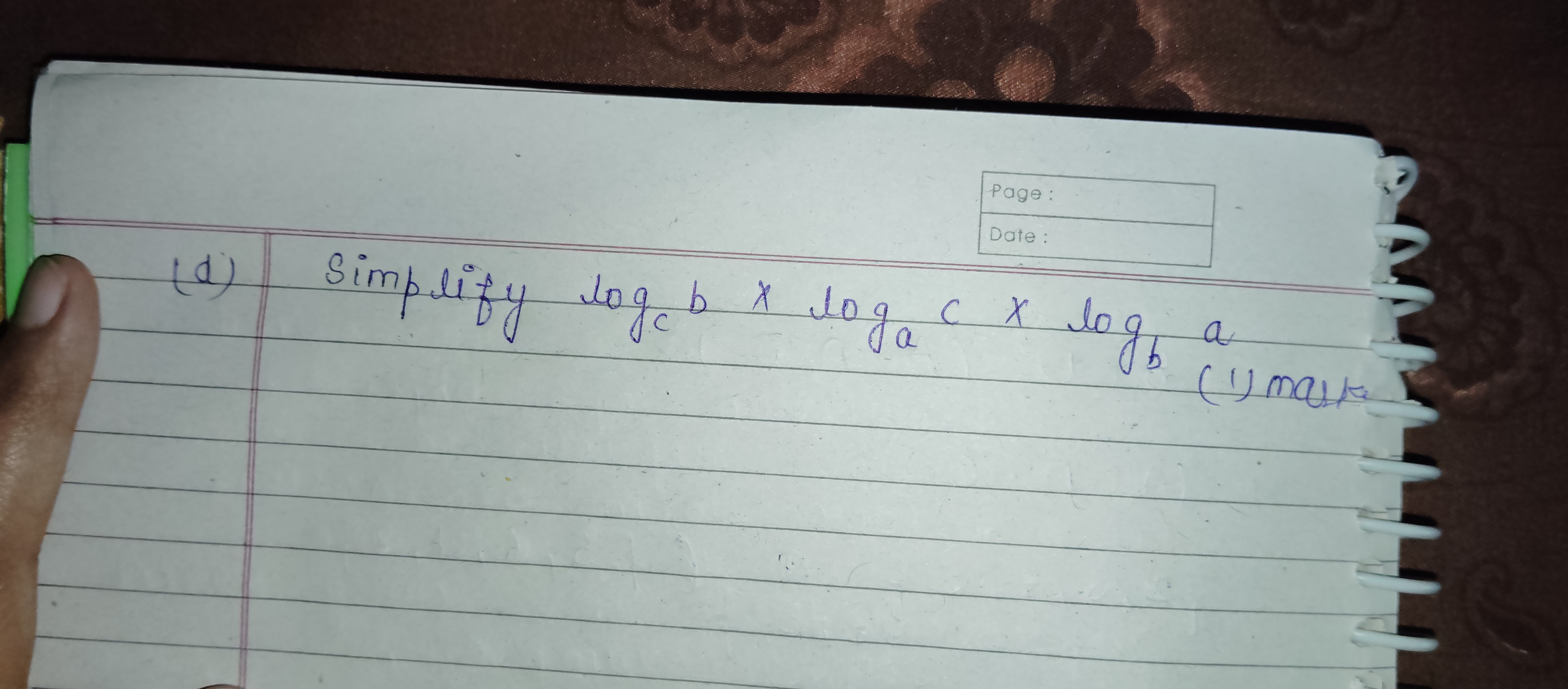
Understand the Problem
The question is asking to simplify the expression involving logarithms: log_c b × log_a c × log_b a. It will require applying logarithmic properties to reduce it to a simpler form.
Answer
1
Answer for screen readers
The simplified expression is: $$ 1 $$
Steps to Solve
-
Apply the Change of Base Formula We can use the change of base formula for logarithms, which states: $$ \log_a b = \frac{\log_c b}{\log_c a} $$
-
Rewrite Each Logarithm Using the change of base formula, we can express each logarithm:
- Rewrite $\log_c b$ as $\frac{\log_a b}{\log_a c}$,
- This means: $$ \log_c b = \frac{\log_a b}{\log_a c} $$
- Similarly, we can rewrite $\log_b a$: $$ \log_b a = \frac{\log_c a}{\log_c b} $$
-
Combine the Factors Substitute the rewritten logarithms back into the expression: $$ \log_c b \times \log_a c \times \log_b a $$ becomes: $$ \left( \frac{\log_a b}{\log_a c} \right) \times \log_a c \times \left( \frac{\log_c a}{\log_c b} \right) $$
-
Simplify the Expression Notice that $\log_a c$ cancels out: $$ \frac{\log_a b \times \log_c a}{\log_c b} $$
-
Recognize the Product of Logarithms Here, you can further simplify: $$ \log_c a = \frac{1}{\log_a c} $$ Plugging this back provides: $$ \log_a c \cdot \log_c a = 1 $$ Consequently: $$ \log_c b \times \log_a c \times \log_b a = 1 $$
The simplified expression is: $$ 1 $$
More Information
This result shows that the product of the logarithmic expressions simplifies neatly to 1, highlighting the underlying properties of logarithms and their relationships.
Tips
- Neglecting the Change of Base Formula: Forgetting to apply the change of base could lead to an incorrect simplification.
- Misinterpreting Logarithmic Relationships: Confusing how to manipulate logs can cause complications; always ensure that you understand what each logarithm represents relative to the others.
AI-generated content may contain errors. Please verify critical information