If 0.009 is to 0.01, what is x value?
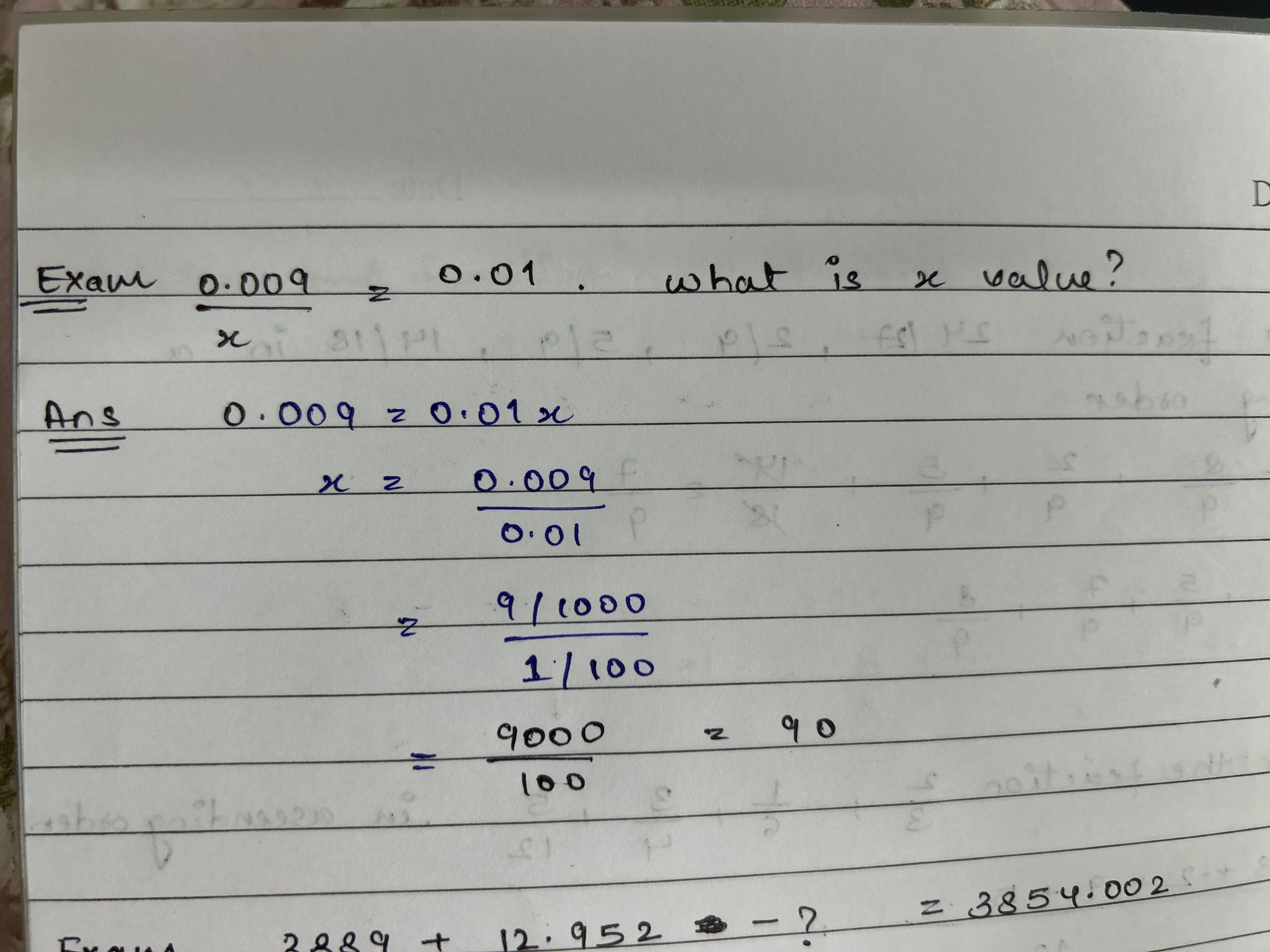
Understand the Problem
The question is asking to solve for the variable 'x' in the equation where 0.009 is to 0.01 as x is to a certain value. It involves proportions and requires solving a basic algebraic equation.
Answer
The value of \( x \) is \( 0.9 \).
Answer for screen readers
The value of ( x ) is ( 0.9 ).
Steps to Solve
- Set up the proportion
Start with the given proportion:
$$ \frac{0.009}{0.01} = \frac{x}{z} $$
Where ( z ) is the value we need to find.
- Cross-multiply
Cross-multiplying the proportion gives:
$$ 0.009 \cdot z = 0.01 \cdot x $$
- Isolate ( x )
Rearranging the equation to solve for ( x ):
$$ x = \frac{0.009 \cdot z}{0.01} $$
- Substituting for ( z )
Assuming we want to evaluate ( x ) for ( z = 1 ) (or any specific value you have in mind), we can do:
If ( z = 1 ):
$$ x = \frac{0.009 \cdot 1}{0.01} $$
- Calculate ( x )
Now calculate ( x ):
$$ x = \frac{0.009}{0.01} = 0.9 $$
The value of ( x ) is ( 0.9 ).
More Information
This problem demonstrates the concept of proportions, where two ratios are set equal to each other. Solving such equations often involves cross-multiplication and isolating the variable.
Tips
- Forgetting to cross-multiply correctly.
- Not simplifying the final answer properly.
- Assuming the wrong value for ( z ) without specifying it.
AI-generated content may contain errors. Please verify critical information