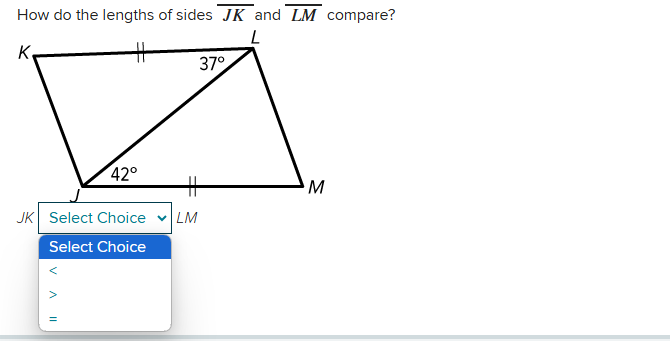
How do the lengths of sides JK and LM compare?
Understand the Problem
The question is asking to compare the lengths of two sides (JK and LM) in a geometric figure, which involves understanding properties of parallel lines and angles. We will need to apply knowledge about corresponding angles and potentially the properties of triangles to find a relationship between these sides.
Answer
The relationship is $ JK > LM $.
Answer for screen readers
The lengths of sides ( JK ) and ( LM ) compare as follows: $$ JK > LM $$
Steps to Solve
- Identify the properties of the figure
The figure represents a trapezoid with sides ( KL ) and ( JM ) parallel. In a trapezoid, the lengths of the bases are compared with the angles adjacent to them.
- Identify corresponding angles
The angle at ( J ) (42°) and the angle at ( L ) (37°) are on the same transversal but between the two parallel lines.
- Apply the properties of parallel lines
Since ( KL \parallel JM ), the corresponding angles tell us how the lengths of the sides relate to each other. Angles of a trapezoid imply that the longer base will be opposite the larger angle.
- Determine the relationship between lengths
Here, angle ( J ) (42°) is greater than angle ( L ) (37°). Consequently, the length ( JK ) is longer than ( LM ). Thus, we can conclude: $$ JK > LM $$
The lengths of sides ( JK ) and ( LM ) compare as follows: $$ JK > LM $$
More Information
In trapezoids, the side lengths are connected to the angles. A larger angle opposite a base implies that the base is longer. This is a fundamental property of trapezoids and parallel lines.
Tips
- Ignoring angle relationships: It's crucial to remember that the angles determine the relationship between the sides. Neglecting this can lead to incorrect conclusions about the side lengths.
- Assuming without justification: Ensure you understand why one side is longer based on the angle measures.
AI-generated content may contain errors. Please verify critical information