Hence, or otherwise, find the smallest positive value of x, where x is in radians, for which the curve with equation y = f(x) has a turning point.
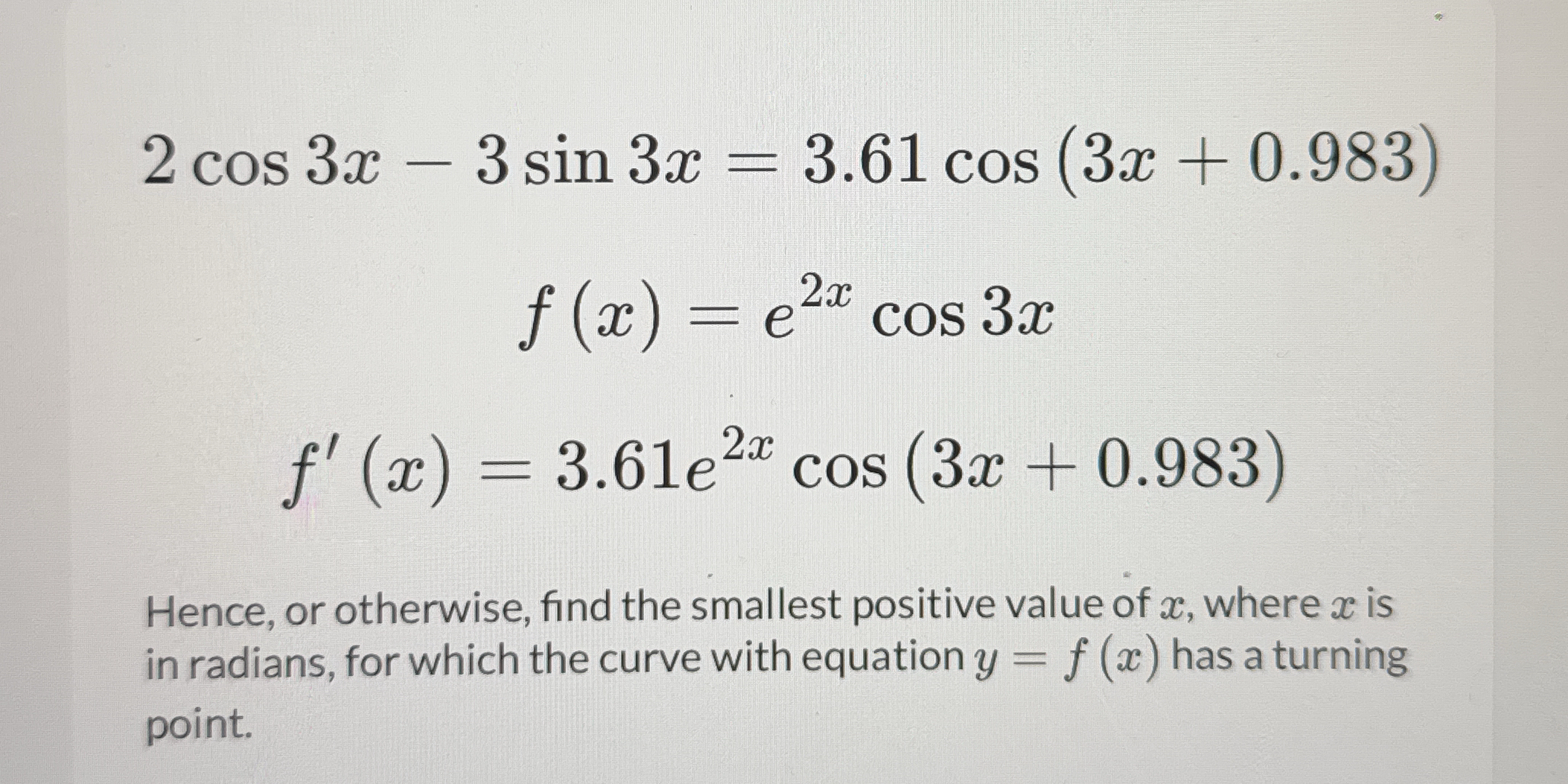
Understand the Problem
The question is asking for the smallest positive value of x, in radians, for which the curve defined by the function f(x) has a turning point. The context involves finding critical points through the derivative f'(x) and setting it equal to zero to determine turning points.
Answer
The smallest positive value of \( x \) is approximately $0.19593$.
Answer for screen readers
The smallest positive value of ( x ) is approximately
$$ x \approx 0.19593 $$
Steps to Solve
- Set the derivative equal to zero
To find the turning points, we need to set the derivative ( f'(x) ) equal to zero:
$$ 3.61 e^{2x} \cos(3x + 0.983) = 0 $$
Since ( e^{2x} ) is never zero, we focus on the cosine term:
$$ \cos(3x + 0.983) = 0 $$
- Solve for ( 3x + 0.983 )
The cosine function equals zero at:
$$ 3x + 0.983 = \frac{\pi}{2} + k\pi, \quad k \in \mathbb{Z} $$
We can rearrange this to find ( x ):
$$ 3x = \frac{\pi}{2} + k\pi - 0.983 $$
Divide by 3:
$$ x = \frac{1}{3} \left( \frac{\pi}{2} + k\pi - 0.983 \right) $$
- Calculate the smallest positive ( x )
Start with ( k = 0 ):
$$ x = \frac{1}{3} \left( \frac{\pi}{2} - 0.983 \right) $$
Calculate this value:
- First, compute ( \frac{\pi}{2} \approx 1.5708 ).
Now, substitute and compute:
$$ x = \frac{1}{3} (1.5708 - 0.983) $$
- Decimal calculation
Calculating it step-by-step:
$$ 1.5708 - 0.983 = 0.5878 $$
Now divide by 3:
$$ x \approx \frac{0.5878}{3} \approx 0.19593 $$
- Try ( k = 1 ) for the next possibility
$$ x = \frac{1}{3} \left( \frac{\pi}{2} + \pi - 0.983 \right) $$
Calculate this for ( k = 1 ):
$$ x = \frac{1}{3} \left( \frac{3\pi}{2} - 0.983 \right) $$
- Calculate this value
Using ( \frac{3\pi}{2} \approx 4.7124 ):
$$ x \approx \frac{1}{3} (4.7124 - 0.983) $$
Calculate:
- First, compute ( 4.7124 - 0.983 = 3.7294 ).
Then divide by 3:
$$ x \approx \frac{3.7294}{3} \approx 1.24313 $$
Now we have two potential values for ( x ): ( 0.19593 ) and ( 1.24313 ). The smallest positive value is:
$$ x \approx 0.19593 $$
The smallest positive value of ( x ) is approximately
$$ x \approx 0.19593 $$
More Information
This value represents the first turning point of the function ( f(x) = e^{2x} \cos(3x) ). Turning points are crucial for understanding the behavior of the function, such as where it changes direction.
Tips
- Not considering ( e^{2x} ) when setting the derivative to zero, since it is always positive.
- Forgetting to check additional values of ( k ); ( k = 0 ) might not always yield the smallest positive ( x ).
AI-generated content may contain errors. Please verify critical information