What is the slope of the line represented by the equation -5x + y = -2?
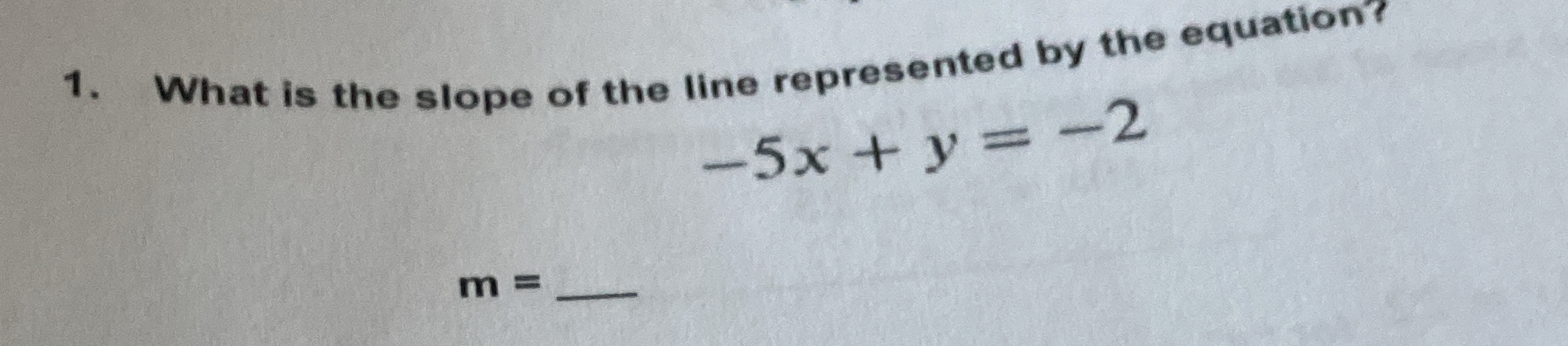
Understand the Problem
The question is asking for the slope of a line represented by a linear equation in standard form. To find the slope, we need to rearrange the equation into slope-intercept form (y = mx + b) where m represents the slope.
Answer
The slope is $m = 5$.
Answer for screen readers
The slope $m$ of the line is $5$.
Steps to Solve
- Rearrange the equation to isolate y We start with the linear equation in standard form: $$ -5x + y = -2 $$
To solve for $y$, we add $5x$ to both sides: $$ y = 5x - 2 $$
- Identify the slope from the slope-intercept form Now that we have the equation in slope-intercept form ($y = mx + b$), we can identify the slope. The slope $m$ is the coefficient of $x$, which in this case is $5$.
The slope $m$ of the line is $5$.
More Information
The slope represents the rate of change of $y$ with respect to $x$. In this case, for every unit increase in $x$, $y$ increases by $5$.
Tips
- Failing to correctly isolate $y$ in the equation, which could lead to confusion about the correct slope.
- Mixing up the signs when rearranging the equation; always double-check each step to avoid sign errors.
AI-generated content may contain errors. Please verify critical information