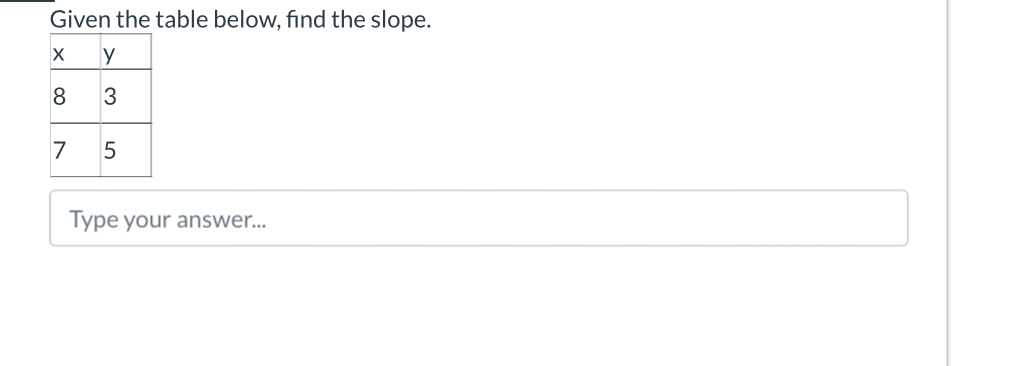
Given the table below, find the slope.
Understand the Problem
The question is asking to calculate the slope given the values of x and y from the provided table. The slope can be found using the formula (y2 - y1) / (x2 - x1) where (x1, y1) and (x2, y2) are two points from the table.
Answer
The slope is $m = -2$.
Answer for screen readers
The slope is $m = -2$.
Steps to Solve
- Identify the Points
The two points from the table are:
- Point 1: $(x_1, y_1) = (8, 3)$
- Point 2: $(x_2, y_2) = (7, 5)$
- Apply the Slope Formula
Use the slope formula:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Substituting the values:
$$ m = \frac{5 - 3}{7 - 8} $$
- Calculate the Numerator
Calculate the difference in y-values:
$$ m = \frac{2}{7 - 8} $$
- Calculate the Denominator
Calculate the difference in x-values:
$$ m = \frac{2}{-1} $$
- Find the Slope
Therefore, the slope is:
$$ m = -2 $$
The slope is $m = -2$.
More Information
The slope represents the rate of change of $y$ with respect to $x$. A negative slope indicates that as $x$ increases, $y$ decreases.
Tips
- Confusing the order of points: Always ensure you correctly assign $(x_1, y_1)$ and $(x_2, y_2)$.
- Not subtracting in the correct order can lead to an incorrect sign for the slope.
AI-generated content may contain errors. Please verify critical information