Given the right triangle below, determine the distance of line segment AB. Round your final answer to the nearest tenth.
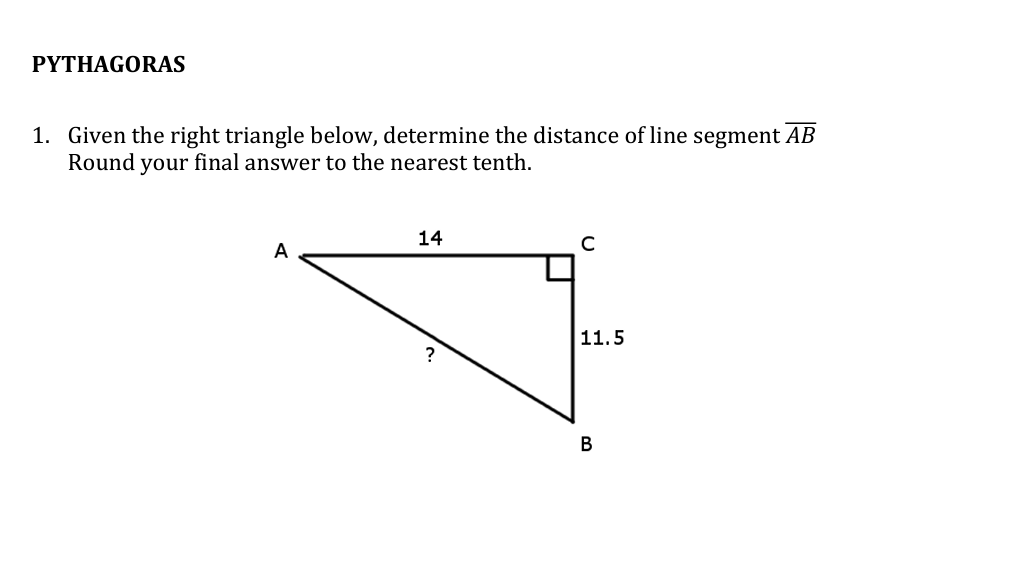
Understand the Problem
The question is asking to determine the distance of line segment AB in a right triangle, given the lengths of the other two sides, using the Pythagorean theorem. We will solve this by applying the formula a² + b² = c².
Answer
The distance of segment $AB$ is approximately $18.1$.
Answer for screen readers
The distance of line segment $AB$ is approximately $18.1$.
Steps to Solve
- Identify the sides of the triangle
In a right triangle, label the sides as follows: let $AB$ be the side we need to find (let's call it $c$), $AC$ be the adjacent side with length 14 (let's call it $a$), and $BC$ be the opposite side with length 11.5 (let's call it $b$).
- Apply the Pythagorean theorem
The Pythagorean theorem states that $a^2 + b^2 = c^2$. Substitute the known lengths into the equation:
$$ 14^2 + 11.5^2 = c^2 $$
- Calculate $14^2$ and $11.5^2$
First, compute the squares of the lengths:
$$ 14^2 = 196 $$
$$ 11.5^2 = 132.25 $$
- Add the results to find $c^2$
Combine the results from the squares:
$$ c^2 = 196 + 132.25 = 328.25 $$
- Find $c$ by taking the square root
Now, take the square root of $c^2$ to find $c$:
$$ c = \sqrt{328.25} $$
- Round the answer to the nearest tenth
Calculate the square root:
$$ c \approx 18.1 $$
The distance of line segment $AB$ is approximately $18.1$.
More Information
This problem uses the Pythagorean theorem, which is fundamental in geometry for finding the lengths of sides in right triangles.
Tips
- Confusing the sides: Make sure to correctly identify which lengths correspond to which sides of the triangle.
- Rounding too early: It's important to perform all calculations before rounding to ensure accuracy in the final answer.
