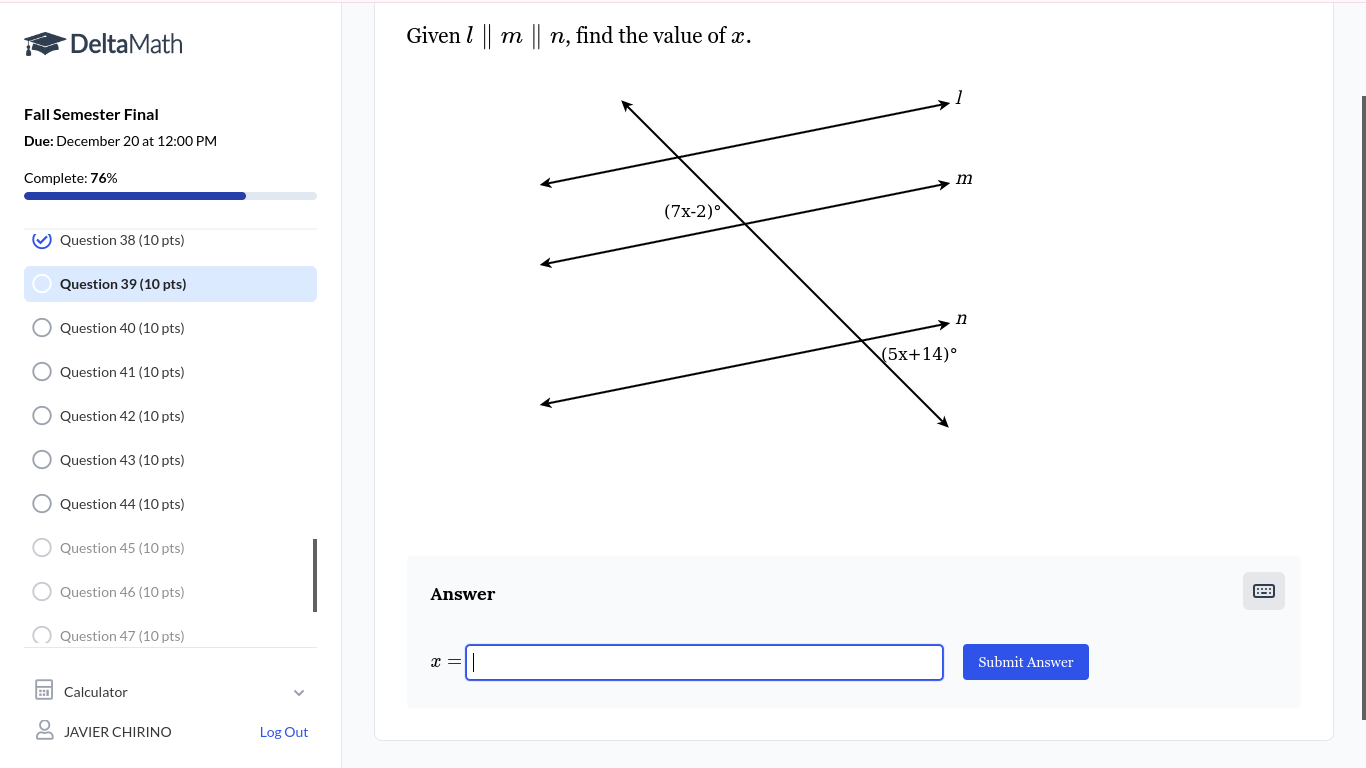
Given l || m || n, find the value of x.
Understand the Problem
The question involves determining the value of x given that lines l, m, and n are parallel. It asks us to use the angle relationships created by the intersecting lines to solve for x.
Answer
The value of \( x \) is \( 8 \).
Answer for screen readers
The value of ( x ) is ( 8 ).
Steps to Solve
-
Identify the Angle Relationships
Since lines ( l ) and ( n ) are parallel and cut by a transversal (line ( m )), we can use alternate interior angles. The angle measuring ( (7x - 2)^\circ ) and the angle measuring ( (5x + 14)^\circ ) are alternate interior angles. -
Set up the Equation
Since alternate interior angles are equal, we can set the two expressions equal to each other:
$$ 7x - 2 = 5x + 14 $$ -
Solve the Equation for ( x )
First, isolate ( x ) by subtracting ( 5x ) from both sides:
$$ 2x - 2 = 14 $$
Now, add ( 2 ) to both sides:
$$ 2x = 16 $$
Finally, divide both sides by ( 2 ):
$$ x = 8 $$
The value of ( x ) is ( 8 ).
More Information
When working with parallel lines and transversals, it's essential to remember the properties of angles: alternate interior angles are equal, corresponding angles are equal, and same-side interior angles are supplementary.
Tips
- Not using the correct angle relationship: Sometimes students forget that alternate interior angles can be used; they might use adjacent or corresponding angles incorrectly.
- Algebraic errors in solving the equation: Forgetting to properly distribute, combine like terms, or make arithmetic mistakes can lead to the wrong answer.
AI-generated content may contain errors. Please verify critical information