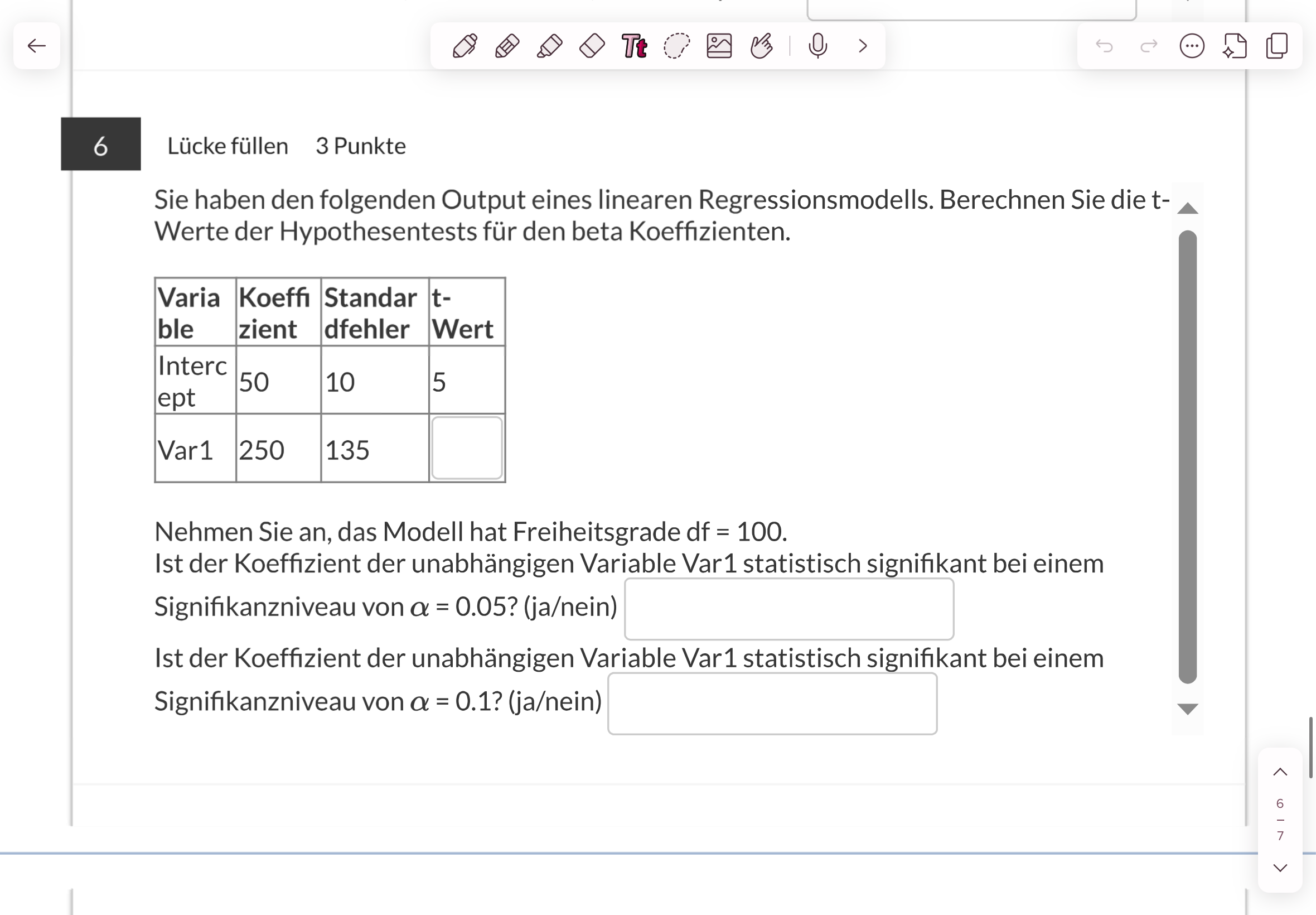
Sie haben den folgenden Output eines linearen Regressionsmodells. Berechnen Sie die t-Werte der Hypothesentests für den beta Koeffizienten. Nehmen Sie an, das Modell hat Freiheitsg... Sie haben den folgenden Output eines linearen Regressionsmodells. Berechnen Sie die t-Werte der Hypothesentests für den beta Koeffizienten. Nehmen Sie an, das Modell hat Freiheitsgrade df = 100. Ist der Koeffizient der unabhängigen Variable Var1 statistisch signifikant bei einem Signifikanzniveau von α = 0.05? (ja/nein) Ist der Koeffizient der unabhängigen Variable Var1 statistisch signifikant bei einem Signifikanzniveau von α = 0.1? (ja/nein)
Understand the Problem
Die Frage verlangt die Berechnung des t-Werts für die unabhängige Variable Var1 in einem linearen Regressionsmodell. Außerdem sollen wir überprüfen, ob der Koeffizient bei gegebenen Signifikanzniveaus statistisch signifikant ist.
Answer
Der t-Wert für Var1 ist ungefähr 1.85. Signifikanz bei $\alpha = 0.05$: nein. Signifikanz bei $\alpha = 0.1$: ja.
Answer for screen readers
Der t-Wert für die unabhängige Variable Var1 beträgt ungefähr 1.85.
- Bei einem Signifikanzniveau von $\alpha = 0.05$ ist der Koeffizient nicht signifikant (nein).
- Bei einem Signifikanzniveau von $\alpha = 0.1$ ist der Koeffizient signifikant (ja).
Steps to Solve
- Berechnung des t-Werts für Var1
Der t-Wert wird berechnet, indem der Koeffizient von Var1 durch seinen Standardfehler geteilt wird:
[ t = \frac{\text{Koeffizient}}{\text{Standardfehler}} = \frac{250}{135} ]
- Berechnung des t-Werts
Führen wir die Berechnung durch:
[ t = \frac{250}{135} \approx 1.85 ]
- Statistische Signifikanz bei einem Signifikanzniveau von $\alpha = 0.05$ prüfen
Für einen t-Wert von 1.85 und 100 Freiheitsgraden (df) wird der kritische t-Wert aus der t-Verteilungstabelle für $\alpha = 0.05$ (zweiseitig) benötigt. Der kritische Wert liegt ungefähr bei ±1.984.
Da $1.85 < 1.984$, ist der Koeffizient statistisch nicht signifikant bei $\alpha = 0.05$.
- Statistische Signifikanz bei einem Signifikanzniveau von $\alpha = 0.1$ prüfen
Für $\alpha = 0.1$ liegt der kritische t-Wert (zweiseitig) bei etwa ±1.660.
Da $1.85 > 1.660$, ist der Koeffizient statistisch signifikant bei $\alpha = 0.1$.
Der t-Wert für die unabhängige Variable Var1 beträgt ungefähr 1.85.
- Bei einem Signifikanzniveau von $\alpha = 0.05$ ist der Koeffizient nicht signifikant (nein).
- Bei einem Signifikanzniveau von $\alpha = 0.1$ ist der Koeffizient signifikant (ja).
More Information
Der t-Test wird verwendet, um zu bestimmen, ob ein Koeffizient in einem Regressionsmodell signifikant von null abweicht. Kritische t-Werte variieren je nach dem gewählten Signifikanzniveau und den Freiheitsgraden.
Tips
- Verwechseln der kritischen t-Werte für verschiedene Signifikanzniveaus. Achte darauf, den richtigen Wert aus der t-Verteilungstabelle zu verwenden.
- Eine falsche Berechnung des t-Werts. Es ist wichtig, den Koeffizienten und den Standardfehler korrekt zu verwenden.
AI-generated content may contain errors. Please verify critical information