[fºl m|z-x|+1=-(x)]/ (m)
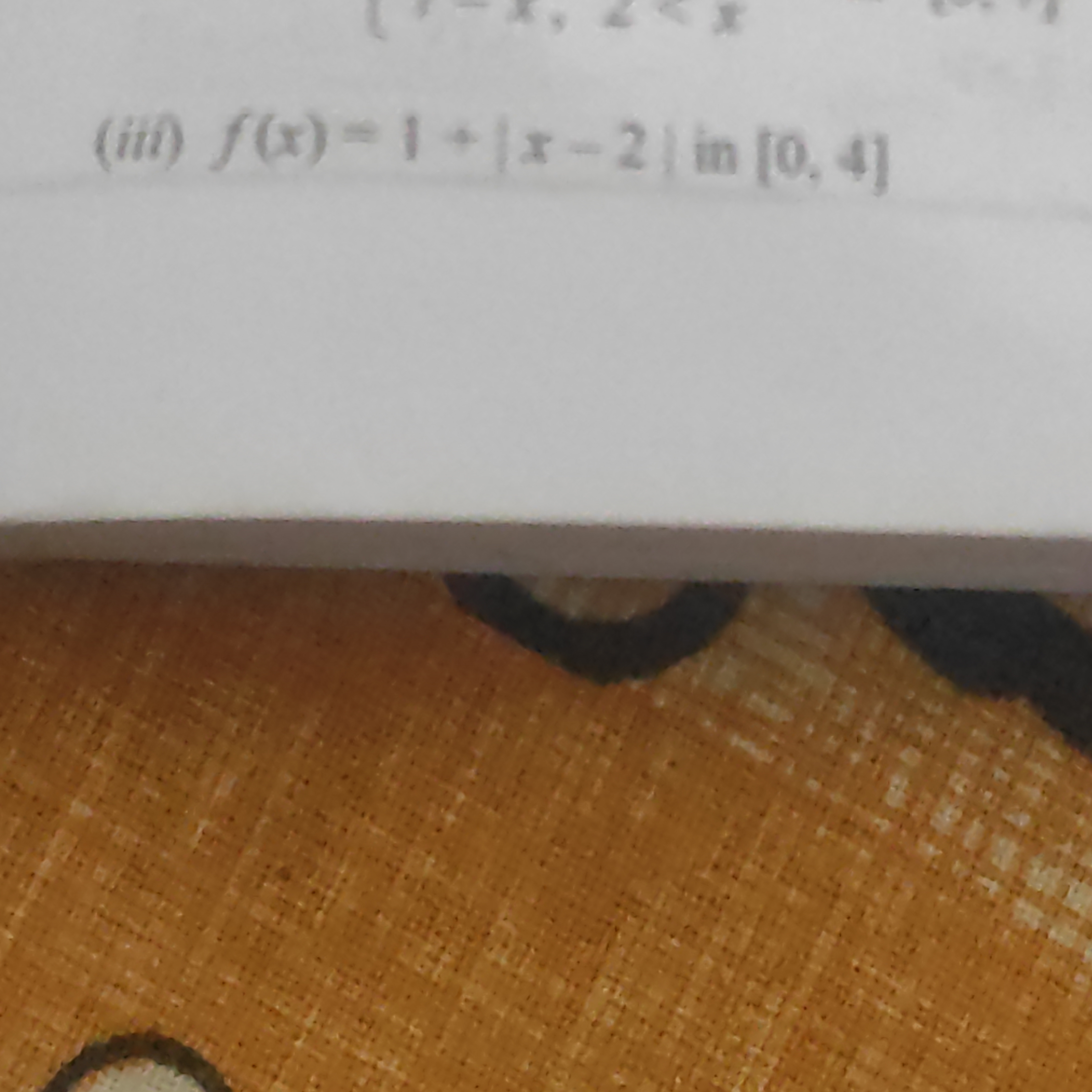
Understand the Problem
The question seems to involve a mathematical expression that includes absolute values and functions. The high-level approach involves analyzing and possibly solving the equation or understanding its properties.
Answer
The solution requires analyzing \( |z - x| \) under cases, leading to different equations for \( x \) based on initial conditions.
Answer for screen readers
The relationship governing ( x ) and ( z ) involves the absolute value equation expressed through two cases, leading to different solutions based on the conditions provided. The complete expressions require solving each case.
Steps to Solve
- Identify the equation structure
The given equation is
$$ \frac{fºl \cdot m |z - x| + 1 = - (x)}{m} $$
We need to analyze the components, particularly the absolute value part ( |z - x| ).
- Isolate the absolute value
Multiply both sides by ( m ) (assuming ( m \neq 0 )) gives us:
$$ fºl \cdot |z - x| + 1 = -mx $$
Next, we isolate ( |z - x| ):
$$ fºl \cdot |z - x| = -mx - 1 $$
- Solve for ( |z - x| )
To isolate ( |z - x| ), divide both sides by ( fºl ):
$$ |z - x| = \frac{-mx - 1}{fºl} $$
This indicates that ( |z - x| ) must be non-negative, leading us to a constraint on ( x ).
- Analyze Cases for Absolute Value
We need to consider two cases based on the definition of absolute value:
Case 1: ( z - x \geq 0 )
Here, we have:
$$ z - x = \frac{-mx - 1}{fºl} $$
Case 2: ( z - x < 0 )
Here, we rewrite the absolute value:
$$ -(z - x) = \frac{-mx - 1}{fºl} $$
- Solve each case
For each case, we will solve for ( x ) in terms of ( z ) and other variables.
For Case 1:
$$ z - x = \frac{-mx - 1}{fºl} $$
Rearranging:
$$ z = x + \frac{-mx - 1}{fºl} $$
This can be further simplified to solve for ( x ).
For Case 2:
$$ -x + z = \frac{-mx - 1}{fºl} $$
Rearranging gives a different equation for ( x ).
The relationship governing ( x ) and ( z ) involves the absolute value equation expressed through two cases, leading to different solutions based on the conditions provided. The complete expressions require solving each case.
More Information
The expression integrates absolute values and requires careful handling as it can lead to different valid conditions based on the signs of expressions involved. Absolute value problems often have multiple solutions due to the nature of their definitions.
Tips
- Neglecting to consider both cases when solving absolute value equations.
- Forgetting that absolute values are always non-negative and thus providing negative outputs could lead to contradictions.
- Mismanaging sign changes during the algebraic manipulation.
AI-generated content may contain errors. Please verify critical information