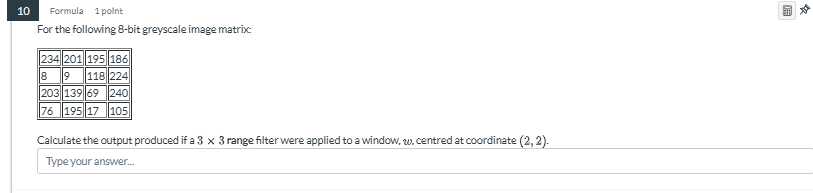
Calculate the output produced if a 3 x 3 range filter were applied to a window, centered at coordinate (2,2).
Understand the Problem
The question is asking for the output of applying a 3x3 range filter to a specified portion of a grayscale image matrix. The filter needs to be calculated at the coordinates given (2,2), referring to the center of the window in the matrix provided.
Answer
231
Answer for screen readers
The output produced by the 3x3 range filter is 231.
Steps to Solve
- Identify the window of the filter To apply a 3x3 range filter centered at coordinate (2, 2), we need to extract the 3x3 matrix from the image matrix. The coordinates (2, 2) refer to the third row and third column (zero-indexed).
The 3x3 window around (2, 2) is:
$$
\begin{bmatrix}
201 & 195 & 186 \
9 & 118 & 224 \
139 & 69 & 240
\end{bmatrix}
$$
- Flatten the window Next, we will flatten this 3x3 window into a single list for easier computation.
Flattened window:
$$ [201, 195, 186, 9, 118, 224, 139, 69, 240] $$
- Calculate the range of pixel values The range filter typically calculates the difference between the maximum and minimum values within the window.
Maximum value: $$ \text{max} = 240 $$
Minimum value: $$ \text{min} = 9 $$
-
Compute the output
The output of the range filter is calculated as follows:
$$ \text{output} = \text{max} - \text{min} $$
Substituting the values we calculated: $$ \text{output} = 240 - 9 = 231 $$
The output produced by the 3x3 range filter is 231.
More Information
The range filter is a significant operation in image processing that helps in edge detection and noise reduction by assessing the variability of pixel values within a neighborhood. Higher output values indicate greater contrast in the surrounding pixel values.
Tips
- Forgetting to correctly extract the 3x3 window, which could lead to incorrect calculations.
- Misidentifying the maximum and minimum values. Always double-check these values in the extracted window.
AI-generated content may contain errors. Please verify critical information