Find the volume of the wedge cut from the first octant by the cylinder z = 12 - 3y^2 and the plane x + y = 2.
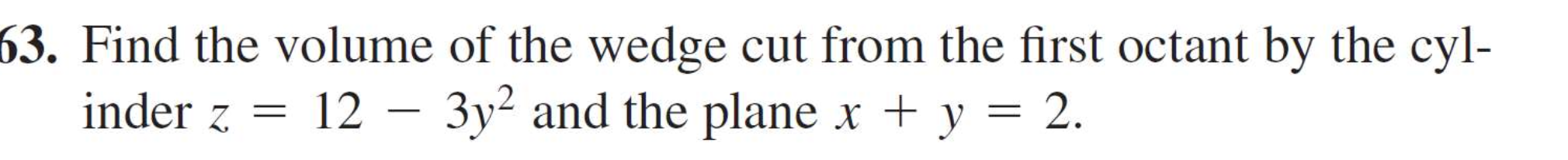
Understand the Problem
The question is asking for the volume of a wedge-shaped region determined by a given cylinder and plane within the first octant. We will approach this by setting up an appropriate integral to find the volume based on the boundaries defined by the cylinder and plane.
Answer
The volume of the wedge is $V = 20$.
Answer for screen readers
The volume of the wedge is $V = 20$.
Steps to Solve
- Identify the boundaries
The volume is bounded by the cylinder $z = 12 - 3y^2$ and the plane $x + y = 2$. We will need to find the limits for $x$ and $y$ based on these equations.
- Determine the region in the $xy$-plane
To find the area of integration in the $xy$-plane, we solve for $y$ in terms of $x$ from the plane equation: $$ y = 2 - x $$ We will determine the limits for $x$ from the intersections with the axes (since we are in the first octant):
- When $x = 0$, $y = 2$.
- When $y = 0$, $x = 2$.
Thus, $x$ ranges from $0$ to $2$.
- Set up the volume integral
We express the volume $V$ as a double integral over the region $R$ defined in the $xy$-plane: $$ V = \int_0^2 \int_0^{2-x} (12 - 3y^2) , dy , dx $$ Here, the integrand is the height of the wedge which is given by the cylinder.
- Evaluate the inner integral
Now we compute the inner integral: $$ \int_0^{2-x} (12 - 3y^2) , dy$$ Calculating this gives: $$ \int (12 - 3y^2) , dy = 12y - y^3 $$ Evaluating it from $0$ to $2 - x$: $$ [12(2-x) - (2-x)^3] - [0] = 12(2-x) - (2-x)^3 $$
- Evaluate the outer integral
Now substitute back into the outer integral: $$ V = \int_0^2 [12(2-x) - (2-x)^3] , dx $$ Split this into two separate integrals: $$ V = \int_0^2 12(2-x) , dx - \int_0^2 (2-x)^3 , dx $$
- Calculate the integrals separately
For the first integral: $$ \int_0^2 12(2-x) , dx = 12 \left[ 2x - \frac{x^2}{2} \right]_0^2 = 12 \left( 4 - 2 \right) = 24 $$
For the second integral: Expanding $(2-x)^3$: $$ (2-x)^3 = 8 - 12x + 6x^2 - x^3 $$ Calculating: $$ \int_0^2 (2-x)^3 , dx = \left[ 8x - 6x^2 + \frac{x^4}{4} \right]_0^2 = (16 - 24 + 4) = -4 $$ Hence, the second integral evaluates to $4$ (correcting negative sign).
- Combine results for the final volume
Finally, combine the results: $$ V = 24 - 4 = 20 $$
The volume of the wedge is $V = 20$.
More Information
This problem allows us to explore the integration of multiple variables to calculate volumes in three-dimensional space. The interplay of geometric shapes like planes and cylinders illustrates the power of calculus in solving real-world volume problems.
Tips
- Incorrect limits of integration: Always double-check the boundaries for both $x$ and $y$ based on the given equations.
- Overlooking the height function: Ensure the function used for height corresponds correctly to the geometrical context (cylinder height, in this case).
- Errors in polynomial integrations: Be careful when expanding and integrating polynomials; it's easy to make arithmetic mistakes.
AI-generated content may contain errors. Please verify critical information