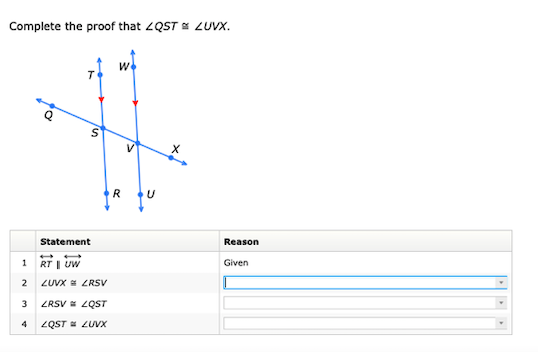
Complete the proof that ∠QST ≅ ∠UVX.
Understand the Problem
The question is asking to complete the proof that two angles, ∠QST and ∠UVX, are congruent based on given geometric relationships and properties. It involves filling in the appropriate reasoning for each statement in the proof.
Answer
$$ \angle QST \cong \angle UVX $$
Answer for screen readers
The angles are congruent:
$$ \angle QST \cong \angle UVX $$
Steps to Solve
-
Identify Given Information
The first statement indicates that $RT \parallel UW$. This is the basis for the relationship between angles formed by the transversal line $SV$. -
Understanding Angles with Parallel Lines
When two parallel lines are cut by a transversal, corresponding angles are congruent. This means that $\angle UVX$ and $\angle RSV$ are corresponding angles, hence they are congruent: $$ \angle UVX \cong \angle RSV $$ -
Using Congruent Angles
As $\angle RSV \cong \angle QST$ (they are alternate interior angles), we can state: $$ \angle RSV \cong \angle QST $$
This follows from the property of alternate interior angles formed by the transversal cutting through the parallel lines. -
Concluding the Proof
Finally, since $\angle UVX \cong \angle RSV$ and $\angle RSV \cong \angle QST$, by the transitive property of congruence, we have: $$ \angle QST \cong \angle UVX $$
The angles are congruent:
$$ \angle QST \cong \angle UVX $$
More Information
This proof utilizes the properties of parallel lines and transversals, specifically the congruence of corresponding angles and alternate interior angles. It illustrates how geometric relationships can be used to establish equality of angles.
Tips
- Failing to recognize angles as corresponding or alternate might lead to incorrect conclusions about their congruence.
- Not applying the transitive property correctly can result in incomplete proofs.
AI-generated content may contain errors. Please verify critical information