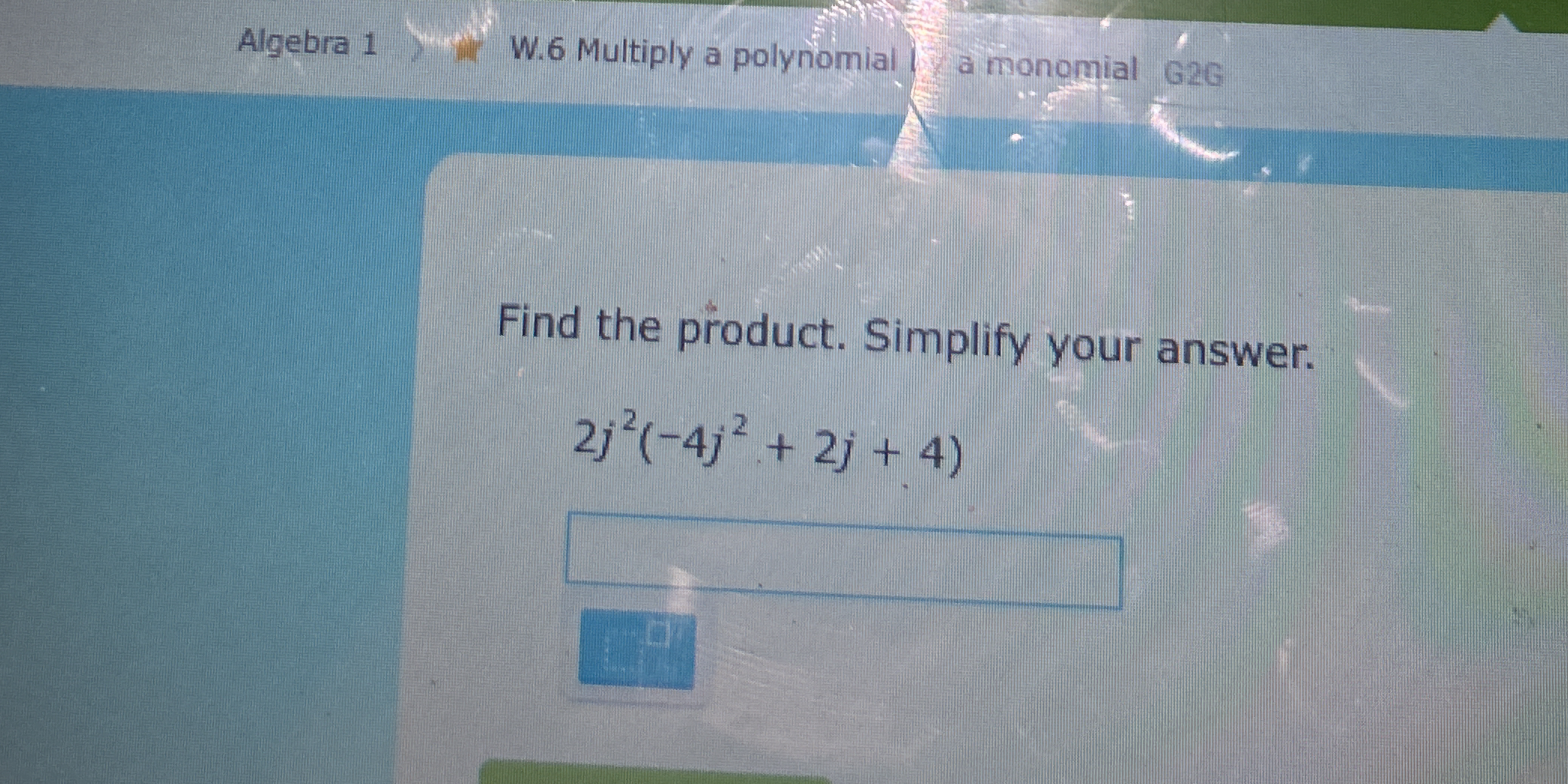
Find the product. Simplify your answer: 2j^2(-4j^2 + 2j + 4)
Understand the Problem
The question is asking to find the product of the expression by multiplying the polynomial and simplifying the result.
Answer
The product is \( -8j^4 + 4j^3 + 8j^2 \).
Answer for screen readers
The final simplified product is:
$$ -8j^4 + 4j^3 + 8j^2 $$
Steps to Solve
- Identify the expression to multiply
The expression is (2j^2(-4j^2 + 2j + 4)).
- Distribute (2j^2) to each term in the polynomial
Multiply (2j^2) by each term inside the parentheses:
- (2j^2 \times -4j^2 = -8j^4)
- (2j^2 \times 2j = 4j^3)
- (2j^2 \times 4 = 8j^2)
- Write out the results of the distribution
Combining the results, we have: $$ -8j^4 + 4j^3 + 8j^2 $$
- Rearrange in standard form
Arrange the terms in descending order of the exponent: $$ -8j^4 + 4j^3 + 8j^2 $$
The final simplified product is:
$$ -8j^4 + 4j^3 + 8j^2 $$
More Information
This expression illustrates the distributive property of multiplication over addition. Each term from the polynomial is multiplied by the monomial, demonstrating how to expand polynomials effectively.
Tips
- Forgetting to multiply all terms in the polynomial by the coefficient outside the parentheses.
- Mixing up the signs during the multiplication process.
- Not arranging the final expression in standard form.
AI-generated content may contain errors. Please verify critical information