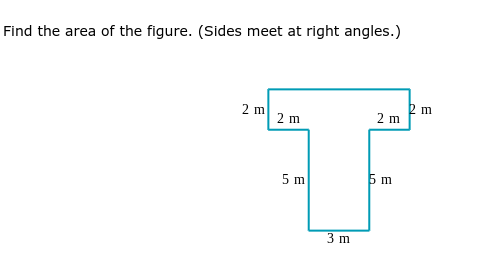
Find the area of the figure. (Sides meet at right angles.)
Understand the Problem
The question is asking us to calculate the area of the given T-shaped figure. The dimensions of the figure are provided, and the sides meet at right angles, which gives us the necessary information to break the shape into simpler rectangles for area calculation.
Answer
The area of the figure is $23 \, \text{m}^2$.
Answer for screen readers
The area of the T-shaped figure is $23 , \text{m}^2$.
Steps to Solve
-
Identify the T-shape dimensions
The T-shape can be divided into two rectangles: one horizontal rectangle on top and one vertical rectangle in the middle. -
Calculate the area of the horizontal rectangle
The dimensions of the horizontal rectangle are:
- Width: $2 , \text{m} + 2 , \text{m} = 4 , \text{m}$ (sum of the top widths)
- Height: $2 , \text{m}$
The area can be calculated using the formula for the area of a rectangle:
$$ \text{Area}_{\text{horizontal}} = \text{width} \times \text{height} = 4 , \text{m} \times 2 , \text{m} = 8 , \text{m}^2 $$
-
Calculate the area of the vertical rectangle
The dimensions of the vertical rectangle are:
- Width: $3 , \text{m}$
- Height: $5 , \text{m}$
The area is calculated as follows:
$$ \text{Area}_{\text{vertical}} = \text{width} \times \text{height} = 3 , \text{m} \times 5 , \text{m} = 15 , \text{m}^2 $$
-
Calculate the total area of the T-shape
To find the total area, sum the areas of both rectangles:
$$ \text{Total Area} = \text{Area}{\text{horizontal}} + \text{Area}{\text{vertical}} = 8 , \text{m}^2 + 15 , \text{m}^2 = 23 , \text{m}^2 $$
The area of the T-shaped figure is $23 , \text{m}^2$.
More Information
The T-shaped figure combines the areas of two rectangles, making it easier to calculate the total area by breaking it down into manageable parts. Understanding how to divide complex shapes into simpler ones is a key skill in geometry.
Tips
- Miscalculating dimensions when summing widths; always double-check the individual parts' contributions to total dimensions.
- Forgetting to add the areas of both shapes when calculating the total area.
AI-generated content may contain errors. Please verify critical information