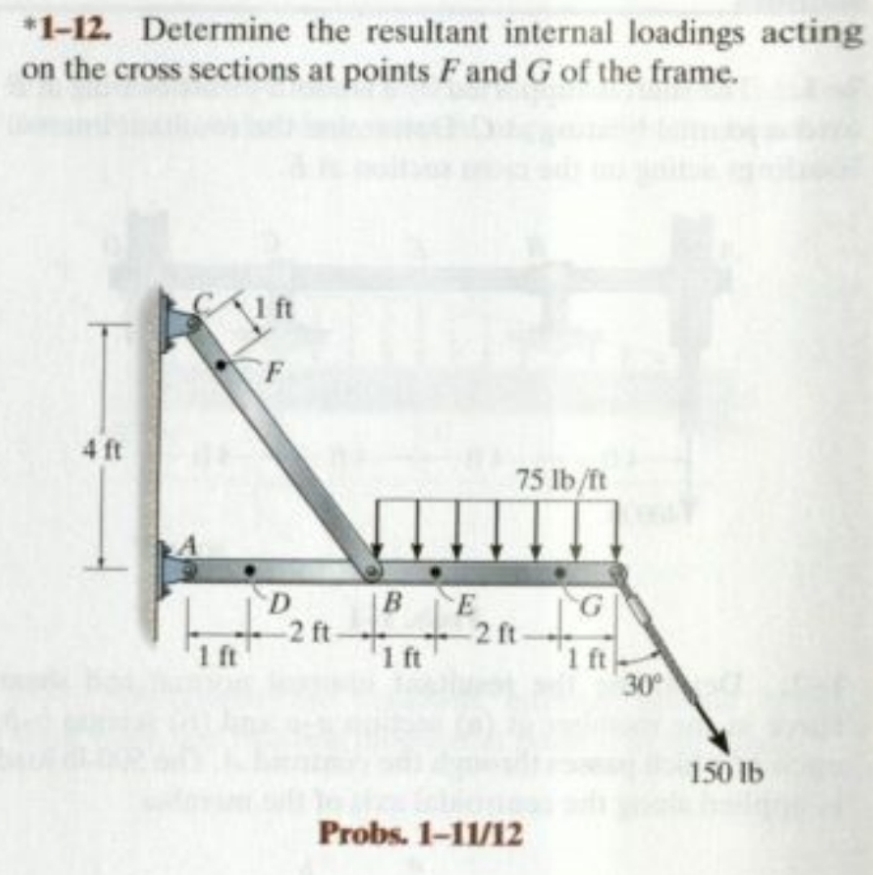
Determine the resultant internal loadings acting on the cross sections at points F and G of the frame.

Steps to Solve

1. Identify the Forces Acting on the Frame

We need to identify all forces acting on the structure, which includes the distributed load and the applied loads. The distributed load on segment ( AB ) is ( 75 , \text{lb/ft} ). The total load on this segment, calculated over ( 4 , \text{ft} ) is:

$$ W_{AB} = 75 , \text{lb/ft} \times 4 , \text{ft} = 300 , \text{lb} $$

2. Calculate the Location of the Resultant Force from the Distributed Load

The resultant force acts at the centroid of the distributed load over the length of ( 4 , \text{ft} ). For a uniform load, the centroid is at the midpoint:

$$ \text{Distance from A} = \frac{4 , \text{ft}}{2} = 2 , \text{ft} $$

Thus, the resultant force ( W_{AB} ) acts at point ( B ) which is ( 2 , \text{ft} ) from point ( A ).

3. Determine External Reactions at Supports

Next, we apply the static equilibrium conditions to find the reactions at the supports. Taking moments about point ( A ) (consider clockwise moments as positive):

$$ \sum M_A = 0 = R_C \cdot 4 , \text{ft} - 300 , \text{lb} \cdot (2 , \text{ft}) - 150 , \text{lb} \cdot (5 , \text{ft}) $$

Where ( R_C ) is the reaction at point ( C ) and ( 150 , \text{lb} ) is the load applied at point ( G ).

4. Solve for Support Reactions

Using the moment equation:

[ R_C \cdot 4 = 300 \cdot 2 + 150 \cdot 5 ]

Solving for ( R_C ):

[ R_C = \frac{300 \cdot 2 + 150 \cdot 5}{4} ]

5. Calculate Internal Forces at Sections F and G

At section ( F ):

• Use the equilibrium of forces in the horizontal and vertical directions to find the internal axial force and shear force.

At section ( G ):

• Repeat the same equilibrium analysis for section ( G ) using the calculated reactions to determine any vertical shear or axial force at this cross section.