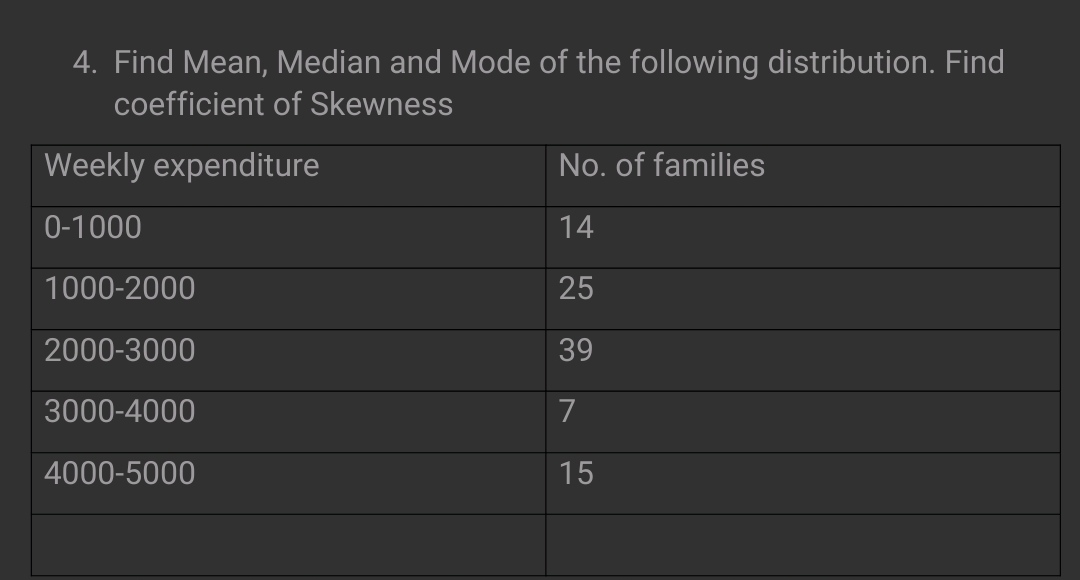
Find Mean, Median and Mode of the following distribution. Find coefficient of Skewness.

Steps to Solve

1. Calculate the Mean

To find the mean of the frequency distribution, use the formula:

$$ \text{Mean} = \frac{\Sigma (f \cdot x)}{N} $$

Where $f$ is the frequency and $x$ is the midpoint of each class interval. First, calculate the midpoint for each class:

• Midpoint for 0-1000: $500$
• Midpoint for 1000-2000: $1500$
• Midpoint for 2000-3000: $2500$
• Midpoint for 3000-4000: $3500$
• Midpoint for 4000-5000: $4500$

Now, calculate $f \cdot x$ for each class:

• For 0-1000: $14 \cdot 500 = 7000$
• For 1000-2000: $25 \cdot 1500 = 37500$
• For 2000-3000: $39 \cdot 2500 = 97500$
• For 3000-4000: $7 \cdot 3500 = 24500$
• For 4000-5000: $15 \cdot 4500 = 67500$

Now find the total of $f$, which is:

$$ N = 14 + 25 + 39 + 7 + 15 = 100 $$

And the sum of $f \cdot x$ is:

$$ \Sigma (f \cdot x) = 7000 + 37500 + 97500 + 24500 + 67500 = 136500 $$

Putting this into the mean formula:

$$ \text{Mean} = \frac{136500}{100} = 1365 $$

2. Calculate the Median

To find the median, identify the cumulative frequency and the median class. The cumulative frequencies are:

• 0-1000: 14
• 1000-2000: 39 (14 + 25)
• 2000-3000: 78 (39 + 39)
• 3000-4000: 85 (78 + 7)
• 4000-5000: 100 (85 + 15)

The median lies in the class where the cumulative frequency equals or exceeds $\frac{N}{2} = 50$.

The median class is 2000-3000.

Now, use the formula:

$$ \text{Median} = L + \left(\frac{\frac{N}{2} - CF}{f}\right) \cdot c $$

Where:

• $L = 2000$ (lower boundary of the median class)
• $CF = 39$ (cumulative frequency before the median class)
• $f = 39$ (frequency of the median class)
• $c = 1000$ (class width)

Substituting in the values:

$$ \text{Median} = 2000 + \left(\frac{50 - 39}{39}\right) \cdot 1000 $$

This gives:

$$ \text{Median} = 2000 + \left(\frac{11}{39}\right) \cdot 1000 \approx 2000 + 282.05 \approx 2282.05 $$

3. Calculate the Mode

The mode is the class with the highest frequency, which is 2000-3000 with a frequency of 39.

Use the mode formula:

$$ \text{Mode} = L + \left(\frac{f_1 - f_0}{2f_1 - f_0 - f_2}\right) \cdot c $$

Where:

• $L = 2000$ (lower boundary of the modal class)
• $f_1 = 39$ (frequency of the modal class)
• $f_0 = 25$ (frequency of the class before the modal class)
• $f_2 = 7$ (frequency of the class after the modal class)
• $c = 1000$

Substituting in the values:

$$ \text{Mode} = 2000 + \left(\frac{39 - 25}{2 \cdot 39 - 25 - 7}\right) \cdot 1000 $$

Calculating this gives:

$$ \text{Mode} = 2000 + \left(\frac{14}{78}\right) \cdot 1000 \approx 2000 + 179.49 \approx 2179.49 $$

4. Calculate the Coefficient of Skewness

The coefficient of skewness can be found using:

$$ \text{Skewness} = \frac{3(\text{Mean} - \text{Median})}{\text{Standard Deviation}} $$

First, calculate the variance and then standard deviation.

• Mean = 1365
• Median = 2282.05

To calculate the variance, we need to determine:

1. Find $(x - \text{Mean})^2 \cdot f$ for each class.
2. Use the formula:

$$ \sigma^2 = \frac{\Sigma (f \cdot (x - \text{Mean})^2)}{N} $$

After completing, plug back into the skewness formula.