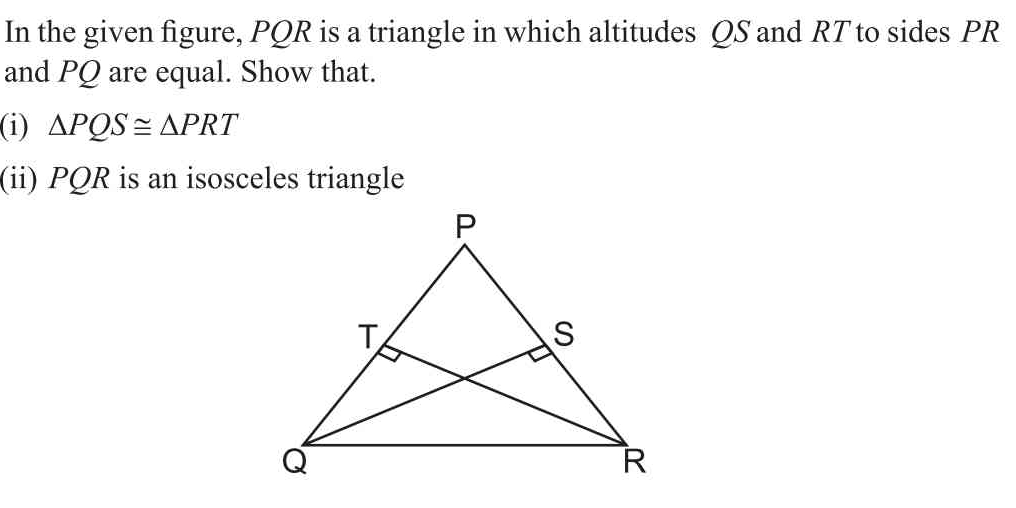
In the given figure, PQR is a triangle in which altitudes QS and RT to sides PR and PQ are equal. Show that (i) triangle PQS ≅ triangle PRT and (ii) triangle PQR is an isosceles tr... In the given figure, PQR is a triangle in which altitudes QS and RT to sides PR and PQ are equal. Show that (i) triangle PQS ≅ triangle PRT and (ii) triangle PQR is an isosceles triangle.
Understand the Problem
The question requires proving two statements about the triangle PQR given that the altitudes QS and RT to its sides PR and PQ are equal. The first part asks to show that triangles PQS and PRT are congruent, and the second part seeks to demonstrate that triangle PQR is isosceles.
Answer
(i) $\triangle PQS \cong \triangle PRT$; (ii) $PQR$ is isosceles.
Answer for screen readers
(i) $\triangle PQS \cong \triangle PRT$
(ii) $PQR$ is an isosceles triangle.
Steps to Solve
- Identify Given Information
We know that triangles PQS and PRT share some important characteristics:
- $QS$ is the altitude of triangle $PQR$ dropped to side $PR$.
- $RT$ is the altitude of triangle $PQR$ dropped to side $PQ$.
- The lengths of these altitudes are equal: $QS = RT$.
- Establish Congruent Triangles
To prove $\triangle PQS \cong \triangle PRT$, we can apply the criteria for congruence.
- Right Angles: Since both QS and RT are altitudes, $\angle PQS$ and $\angle PRT$ are right angles.
- Equal Sides: We have $PQ = PR$ (given that the altitudes are equal) and $QS = RT$.
Thus, by the Right Angle-Hypotenuse-Side (RHS) criterion, the triangles are congruent: $$ \triangle PQS \cong \triangle PRT $$
- Show Triangle PQR is Isosceles
Since we have established that $\triangle PQS$ is congruent to $\triangle PRT$, we know:
- $PQ = PR$ by the congruence of triangles.
This indicates that the sides opposite the equal angles (PQ and PR) are equal.
Thus, we conclude that triangle $PQR$ is isosceles: $$ PQR \text{ is isosceles} $$
(i) $\triangle PQS \cong \triangle PRT$
(ii) $PQR$ is an isosceles triangle.
More Information
The conclusion that triangles are congruent based on equal altitudes leads to the realization that the triangle is isosceles due to the properties of triangle congruency. This illustrates fundamental concepts in geometry regarding right triangles and congruence criteria.
Tips
- Misidentifying the triangles: Ensure the correct labeling of angles and sides in triangles.
- Confusing altitude with other line segments: Remember that altitudes form right angles with the sides they intersect.
AI-generated content may contain errors. Please verify critical information