Find lim x→-2 h(x).
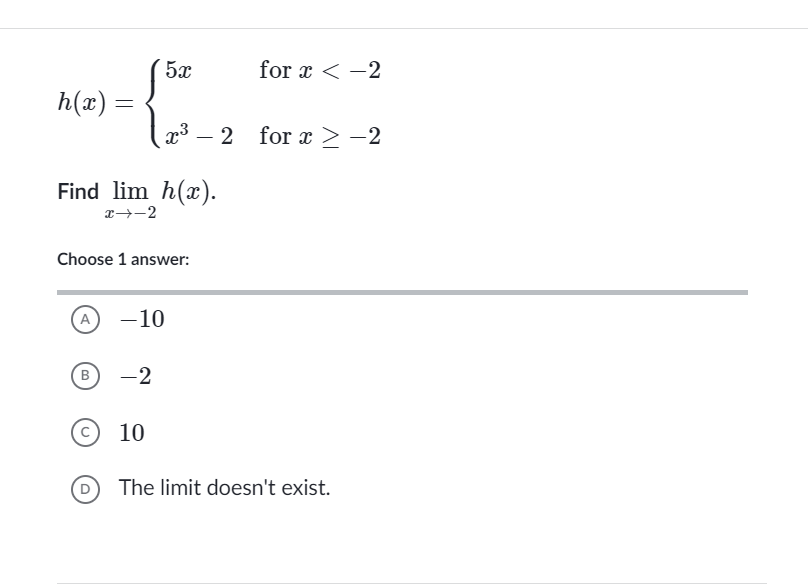
Understand the Problem
The question is asking for the limit of the function h(x) as x approaches -2. The function is piecewise, meaning it has different expressions based on the value of x, and we need to evaluate the limit from both sides of -2 to determine the result.
Answer
The limit as $x$ approaches $-2$ is $-10$.
Answer for screen readers
The limit is $-10$.
Steps to Solve
- Evaluate the limit from the left side
To find the limit of $h(x)$ as $x$ approaches $-2$ from the left ($x \to -2^-$), we use the expression for $h(x)$ when $x < -2$. This is given by:
$$ h(x) = 5x $$
Now, plug in $x = -2$:
$$ h(-2) = 5(-2) = -10 $$
- Evaluate the limit from the right side
Next, we calculate the limit as $x$ approaches $-2$ from the right ($x \to -2^+$). We use the expression for $h(x)$ when $x \geq -2$. This is:
$$ h(x) = x^3 - 2 $$
Again, substitute $x = -2$:
$$ h(-2) = (-2)^3 - 2 = -8 - 2 = -10 $$
- Check if the limits are equal
Since both the limits from the left and the right are equal:
$$ \lim_{x \to -2^-} h(x) = -10 $$
$$ \lim_{x \to -2^+} h(x) = -10 $$
Thus, the overall limit exists and is given by:
$$ \lim_{x \to -2} h(x) = -10 $$
The limit is $-10$.
More Information
In the context of limits for piecewise functions, both one-sided limits must be equal for the overall limit to exist. Here, we found that both sides approached $-10$, confirming the limit.
Tips
Common mistakes include:
- Forgetting to evaluate the one-sided limits separately.
- Miscalculating the function values when plugging in the limits.
AI-generated content may contain errors. Please verify critical information