Complete the square to re-write the quadratic function in vertex form: y = x^2 + 2x + 6
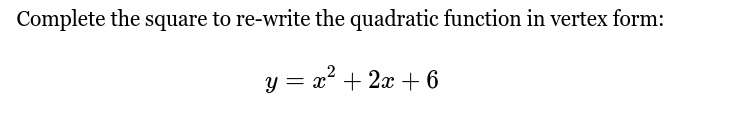
Understand the Problem
The question is asking to rewrite the given quadratic function in its vertex form by completing the square.
Answer
The vertex form is given by $y = (x + 1)^2 + 5$.
Answer for screen readers
The vertex form of the quadratic function is:
$$ y = (x + 1)^2 + 5 $$
Steps to Solve
- Identify the quadratic expression
Start with the quadratic function given:
$$ y = x^2 + 2x + 6 $$
- Isolate the constant
We want to focus on the $x$ terms. To do this, we isolate the constant on the right side:
$$ y - 6 = x^2 + 2x $$
- Complete the square
To complete the square for the expression $x^2 + 2x$, we take half of the coefficient of $x$, which is $2$. Half of $2$ is $1$, and squaring it gives $1$. We will add and subtract this value inside the equation:
$$ y - 6 = (x^2 + 2x + 1 - 1) $$
This simplifies to:
$$ y - 6 = (x + 1)^2 - 1 $$
- Rearrange the equation
Next, we rearrange to express $y$ in vertex form:
$$ y = (x + 1)^2 - 1 + 6 $$
Combine the constants:
$$ y = (x + 1)^2 + 5 $$
- Final vertex form
The vertex form of the quadratic function is:
$$ y = (x + 1)^2 + 5 $$
The vertex form of the quadratic function is:
$$ y = (x + 1)^2 + 5 $$
More Information
The vertex form of a quadratic function is useful for identifying the vertex of the parabola. In this case, the vertex is at the point $(-1, 5)$.
Tips
- Forgetting to balance the equation when completing the square.
- Incorrectly calculating half of the $x$ coefficient.
- Neglecting to combine constants after completing the square.
AI-generated content may contain errors. Please verify critical information